《2025年小题狂做高中数学必修第二册人教版》

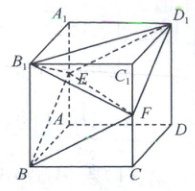
7. 如图，已知正方体 $ABCD - A_1B_1C_1D_1$ 的棱长为 2，$E$，$F$ 分别为棱 $AA_1$，$CC_1$ 的中点，以下结论正确的是(ACD)

A.$V_{三棱锥 B_1 - EFB} = V_{三棱锥 B_1 - EFD_1}$
B.四棱锥 $B_1 - EBFD_1$ 为正四棱锥
C.四棱锥 $B_1 - EBFD_1$ 的体积为 $\frac{8}{3}$
D.多面体 $BCCD_1EF$ 的体积为 $\frac{10}{3}$

答案： 7. ACD 由已知得$EB = BF = FD_1 = D_1E = \sqrt{5}$，$D_1F // BE$，则四边形$EBFD_1$是菱形.对于A，两个三棱锥等底同高，所以$V_{三棱锥B - EFB} = V_{三棱锥B - EFD_1}$，所以A正确；对于B，明显底面$EBFD_1$不是正方形，所以B错误；对于C，$V_{四棱锥B - EBFD_1} = 2V_{三棱锥B - EFB} = 2V_{三棱锥F - B_1EB} = 2 × \frac{1}{3} S_{\triangle EB_1D_1} × 2 = 2 × \frac{1}{3} × 2 × 2 = \frac{8}{3}$，故C正确；对于D，多面体$BCDD_1EF$的体积等于正方体体积一半减去三棱锥$B - ADE$的体积，即$V = \frac{1}{2} × 2 × 2 × 2 - \frac{1}{3} × \frac{1}{2} × 2 × 1 × 2 = \frac{10}{3}$，故D正确.

8. “堑堵”“阳马”和“鳖臑”是我国古代对一些特殊几何体的称谓.《九章算术·商功》：“斜解立方，得两堑堵，斜解堑堵，其一为阳马，其一为鳖臑”. 一个长方体沿对角面斜解(图 1)，得到一模一样的两个堑堵(图 2)，再沿一个堑堵的一个顶点和相对的棱斜解(图 2)，得一个四棱锥称为阳马(图 3)，一个三棱锥称为鳖臑(图 4). 若长方体的体积为 $V$，由该长方体斜解所得到的堑堵、阳马和鳖臑的体积分别为 $V_1$，$V_2$，$V_3$，则下列选项正确的是(ACD)

A.$V_1 + V_2 + V_3 = V$
B.$V_1 = 2V_2$
C.$V_2 = 2V_3$
D.$V_3 = \frac{1}{6}V$

答案： 8. ACD 设长方体的长宽高分别为$a$，$b$，$c$，$V = abc$，则$V_1 = \frac{V}{2} = \frac{1}{2}abc$，$V_2 = \frac{1}{3} × abc = \frac{1}{3}abc$，$V_3 = \frac{1}{3} × \frac{1}{2} × abc = \frac{1}{6}abc$，故$V_1 + V_2 + V_3 = abc = V$，$V_1 = \frac{3}{2}V_2$，$V_2 = 2V_3$，$V_3 = \frac{1}{6}V$，故B错误，A，C，D正确.

9. 如图，在直三棱柱 $\triangle ABC - A_1B_1C_1$ 中，$AB = 2$，$BC = 3$，$CC_1 = 4$，且 $AB \perp BC$，$P$ 为 $BC_1$ 的中点，则(ACD)

A.三棱锥 $A - BCC_1$ 的体积为 4
B.三棱锥 $C - APC_1$ 的体积为 $\frac{5}{2}$
C.四棱锥 $C_1 - ABB_1A_1$ 的体积为 8
D.三棱锥 $C_1 - ABC$ 的表面积为 $14 + 2\sqrt{13}$

答案：
9. ACD 对于A，$V_{A - BC_1D} = V_{C - ABC} = \frac{1}{3} × CC_1 × S_{\triangle ABC} = \frac{1}{3} × 4 × \frac{1}{2} × 2 × 3 = 4$，故A正确；对于B，$V_{C - APC_1} = V_{A - PCC_1}$，而三棱锥$A - BCC_1$与三棱锥$A - PCC_1$有共同的高，因为$P$为$BC_1$的中点，所以$S_{\triangle PCC_1} = \frac{1}{2} S_{\triangle BCC_1}$，则$V_{A - PCC_1} = \frac{1}{2} V_{A - BCC_1} = \frac{1}{2} × 4 = 2$，故B错误；对于C，$V_{C - AB_1A_1} = V_{ABC - A_1B_1C_1} - V_{C - ABC} = \frac{2}{3}V_{ABC - A_1B_1C_1} = \frac{2}{3} × \frac{1}{2} × 2 × 3 × 4 = 8$，故C正确；对于D，由题可知，$AC = \sqrt{13}$，$AC_1 = \sqrt{29}$，$BC_1 = 5$，则$AB^2 + BC^2 = AC^2$，所以$\triangle ABC$是直角三角形，$AB \perp BC$，则三棱锥$C_1 - ABC$的表面积为$S_{\triangle ABC} + S_{\triangle BCC_1} + S_{\triangle AC_1C} + S_{\triangle ABC_1} = \frac{1}{2} × 2 × 3 + \frac{1}{2} × 3 × 4 + \frac{1}{2} × \sqrt{13} × 4 + \frac{1}{2} × 2 × 5 = 14 + 2\sqrt{13}$，故D正确.

方法总结：立体几何求体积的常用方法：规则几何体用公式法；不规则几何体用割补法，通过对不规则几何体进行分割或补充成规则几何体并求体积，再由规则几何体的体积的和差得解；不便计算的三棱锥用等体积变换法，对该三棱锥进行换底变换使其高易求从而得解.

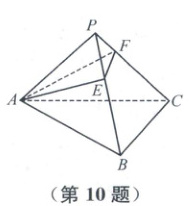
10. 如图，设正三棱锥 $P - ABC$ 的侧棱长为 $l$，$\angle APB = 30°$，$E$，$F$ 分别是 $BP$，$CP$ 上的点，则 $\triangle AEF$ 周长的最小值是$\sqrt{2} : 1$.

答案：
10. $\sqrt{2} : 1$ 将正三棱锥的侧面沿着$AP$展开，得到如图所示的平面图形$PABCA'$，则$AA'$为所求$\triangle AEF$周长的最小值.在$\triangle PAA'$中，$\angle APA' = 90^{\circ}$，$PA = PA' = l$，所以$AA' = \sqrt{2}l$.

方法总结：
(1)求几何体表面上最短距离问题，需将立体图形按所需剪开摊平，从它的侧面展开图寻找所求的最短距离，即利用两点间线段最短来求解.
(2)直棱柱的侧面展开图是矩形；棱锥的侧面展开图是由多个三角形拼成的图形；棱台的侧面展开图是由多个梯形拼成的图形.

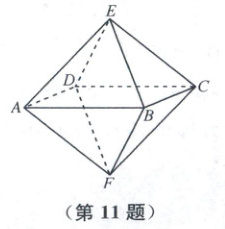
11. 正多面体被古希腊圣哲认为是构成宇宙的基本元素，加上它们的多种变体，一直是科学、艺术、哲学灵感的源泉之一. 如图，该几何体是一个棱长为 2 的正八面体，则此正八面体的体积与表面积之比为$\sqrt{6} : 9$.

答案：
11. $\sqrt{6} : 9$ 如图，由棱长为$2$，可得正八面体上半部分的斜高为$EG = \sqrt{3}$，高为$EO = \sqrt{2}$，则其体积为$2V = 2 × \frac{AB · BC · EO}{3} = \frac{8\sqrt{2}}{3}$，其表面积为$8S = 8 × \frac{EG · BC}{2} = 8\sqrt{3}$，则此正八面体的体积与表面积之比为$\sqrt{6} : 9$.