2025年小题狂做高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
1. (教材变式)已知三个力 $ \boldsymbol{F}_{1}=(-2,-1) $, $ \boldsymbol{F}_{2}=(-3,2) $, $ \boldsymbol{F}_{3}=(7,-3) $ 同时作用于某物体上一点,为使该物体保持平衡,再加上一个力 $ \boldsymbol{F}_{4} $,则 $ \boldsymbol{F}_{4}= $ (
A.$ (-2,-2) $
B.$ (2,-2) $
C.$ (-1,2) $
D.$ (-2,2) $
D
)A.$ (-2,-2) $
B.$ (2,-2) $
C.$ (-1,2) $
D.$ (-2,2) $
答案:
1.D由题意得F1+F2+F3=(−2,−1)+(−3,2)+(7,−3)=(2,−2),要想使该物体保持平衡,只需F4=−(2,−2)=(−2,2).教材链接人教A版必修二习题6.3第2题改编
2. (教材变式)两个力 $ \boldsymbol{F}_{1}=(1,1) $, $ \boldsymbol{F}_{2}=(4,-5) $ 作用于同一个质点,使该点从点 $ A(20,15) $ 移到点 $ B(7,0) $,则这两个力的合力对质点所做的功为 (
A.5
B.$ -5 $
C.10
D.$ -125 $
B
)A.5
B.$ -5 $
C.10
D.$ -125 $
答案:
2.BF=F1+F2=(5,−4),AB=(−13,−15),则W=F·AB=(5,−4)·(−13,−15)=−65+60=−5.教材链接人教A版必修二6.4.2练习第1题改编
3. 若 $ O $ 为 $ \triangle ABC $ 所在平面内一点,且 $ |\overrightarrow{OB}-\overrightarrow{OC}|=|\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}| $,则 $ \triangle ABC $ 为 (
A.等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
D
)A.等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
答案:
3.D由已知得|CB|=|(OB−OA)+(OC−OA)|,则|AB+AC|=|AB−AC|,所以AB²+2AB·AC+AC²=AB²+AC²−2AB·AC,所以AB·AC=0,所以AB⊥AC,即∠BAC=90°,故△ABC为直角三角形.
4. 如图,在梯形 $ ABCD $ 中,$ BC = 3 $,$ AD = 2 $,$ AD // BC $,$ B = \frac{\pi}{3} $,若点 $ M $ 满足 $ 2\overrightarrow{BM}=\overrightarrow{MC} $,点 $ N $ 满足 $ \overrightarrow{DC}=2\overrightarrow{DN} $,且 $ MN=\frac{3\sqrt{3}}{2} $,则 $ AB = $ (

A.3
B.4
C.9
D.12
A
)
A.3
B.4
C.9
D.12
答案:
4.A由题可知MC=2/3BC=2=AD,则四边形AMCD是平行四边形,故DC=AM.又由题意得BM=1/3BC,DN=1/2DC,则AM=BM−BA=1/3BC−BA,AN=AD+DN=AD+1/2DC=2/3BC+1/2AM=2/3BC+1/2(1/3BC−BA)=5/6BC−1/2BA,所以MN=AN−AM=1/2BC+1/2BA,所以|MN|²=1/4(BC+BA)²=1/4(BC²+2BA·BC+BA²)=1/4(9+3|AB|+|AB|²)=27/4,解得|AB|=3或|AB|=−6(舍去).
5. 骑自行车是一种能改善心肺功能的耐力型有氧运动,深受大众喜爱.如图所示是某一型号自行车的平面结构示意图,已知图中自行车的前轮圆 $ A $,后轮圆 $ D $ 的半径均为 $ \sqrt{3} $, $ \triangle ABE $, $ \triangle BEC $, $ \triangle ECD $ 均为边长为 4 的正三角形,设点 $ P $ 为后轮上的一点,则在骑动该自行车的过程中,$ \overrightarrow{AC} · \overrightarrow{BP} $ 的最大值为 (
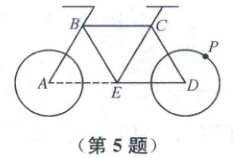
A.12
B.24
C.36
D.48
C
)
A.12
B.24
C.36
D.48
答案:
5.C选择{AB,AE}为基底,因为AC=AB+BC=AB+AE,BP=BD+DP=−AB+2AE+DP,所以AC·BP=−AB²+AB·AE+2AE²+(AB+AE)·DP=24+AC·DP≤24+|AC|·|DP|=36(当且仅当AC,DP同向时等号成立).
6. 在 $ \triangle ABC $ 中,$ \overrightarrow{BC} · \overrightarrow{CA}=\overrightarrow{CA} · \overrightarrow{AB} $,$ |\overrightarrow{BA}+\overrightarrow{BC}|=2\sqrt{3} $,且 $ \frac{\pi}{3} \leqslant B \leqslant \frac{2\pi}{3} $,则 $ \overrightarrow{BA} · \overrightarrow{BC} $ 的取值范围是 (
A.$ [-2,2] $
B.$ [-6,2] $
C.$ \left[-6,\frac{2}{3}\right] $
D.$ \left[-2,\frac{2}{3}\right] $
B
)A.$ [-2,2] $
B.$ [-6,2] $
C.$ \left[-6,\frac{2}{3}\right] $
D.$ \left[-2,\frac{2}{3}\right] $
答案:
6.B如图,取AC中点为D,连接BD,则BC+BA=2BD.又BC·CA=CA·AB,即(BC+BA)·CA=2BD·CA=0,所以BD⊥AC,所以△ABC为等腰三角形.由|BA+BC|=2√3,可得|BD|=√3.因为BA=BD+DA,BC=BD+DC=BD−DA,所以DA·BC=(BD+DA)·(BD−DA)=BD²−DA²=3−|DA|².在Rt△ADB中,tan∠ABD=AD/BD,所以AD=BD·tan∠ABD=√3tan∠ABD.因为∠ABD=1/2∠ABC,且π/3≤∠ABC≤2π/3,所以π/6≤∠ABD≤π/3,则√3/3≤tan∠ABD≤√3,所以1≤AD≤3,从而|DA|²∈[1,9],所以BA·BC=3−|DA|²的取值范围是[−6,2].
6.B如图,取AC中点为D,连接BD,则BC+BA=2BD.又BC·CA=CA·AB,即(BC+BA)·CA=2BD·CA=0,所以BD⊥AC,所以△ABC为等腰三角形.由|BA+BC|=2√3,可得|BD|=√3.因为BA=BD+DA,BC=BD+DC=BD−DA,所以DA·BC=(BD+DA)·(BD−DA)=BD²−DA²=3−|DA|².在Rt△ADB中,tan∠ABD=AD/BD,所以AD=BD·tan∠ABD=√3tan∠ABD.因为∠ABD=1/2∠ABC,且π/3≤∠ABC≤2π/3,所以π/6≤∠ABD≤π/3,则√3/3≤tan∠ABD≤√3,所以1≤AD≤3,从而|DA|²∈[1,9],所以BA·BC=3−|DA|²的取值范围是[−6,2].

7. 在日常生活中,我们常常会看到两个人共提一个行李包的情景,如图,若行李包所受的重力为 $ G $,两个拉力分别为 $ \boldsymbol{F}_{1} $, $ \boldsymbol{F}_{2} $,且 $ |\boldsymbol{F}_{1}|=|\boldsymbol{F}_{2}| $, $ \boldsymbol{F}_{1} $ 与 $ \boldsymbol{F}_{2} $ 夹角为 $ \theta $,当两人拎起行李包时,下列结论正确的是 (
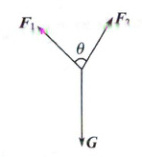
A.$ |\boldsymbol{G}|=|\boldsymbol{F}_{1}|+|\boldsymbol{F}_{0}| $
B.当 $ \theta=\frac{\pi}{2} $ 时,$ |\boldsymbol{F}_{1}|=\frac{\sqrt{2}}{2}|\boldsymbol{G}| $
C.$ \theta $ 越大,越费力
D.当 $ |\boldsymbol{F}_{1}|=|\boldsymbol{G}| $ 时,$ \theta=\frac{\pi}{3} $
BC
)
A.$ |\boldsymbol{G}|=|\boldsymbol{F}_{1}|+|\boldsymbol{F}_{0}| $
B.当 $ \theta=\frac{\pi}{2} $ 时,$ |\boldsymbol{F}_{1}|=\frac{\sqrt{2}}{2}|\boldsymbol{G}| $
C.$ \theta $ 越大,越费力
D.当 $ |\boldsymbol{F}_{1}|=|\boldsymbol{G}| $ 时,$ \theta=\frac{\pi}{3} $
答案:
7.BC根据题意可得G=F1+F2,则|G|=|F1+F2|=√(F1+F2)²=√(F1²+F2²+2F1·F2)=√(2F1²+2F1²cosθ),只有当θ=0时,|G|=2|F1|=|F1|+|F2|,故A错误;当θ=π/2时,|G|=√(2F1²+2F1²cosθ)=√2|F1|,即|F1|=√2/2|G|,故B正确;对于|G|=√(2F1²+2F1²cosθ),因为y=cosθ在(0,π)上单调递减,又因行李包所受的重力G不变,所以当θ越大时,cosθ越小,则越费力,故C正确;当|F1|=|G|时,即|G|=√(2F1²+2F1²cosθ)=|F1|,解得cosθ=−1/2,又因为θ∈(0,π),所以θ=2π/3,故D错误.
查看更多完整答案,请扫码查看


