2025年小题狂做高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
1. 从地面上观察一建在山顶上的建筑物,测得其视角为 $\alpha$,同时测得建筑物顶部仰角为 $\beta$,则山顶的仰角为(
A.$\alpha+\beta$
B.$\alpha-\beta$
C.$\beta-\alpha$
D.$\alpha$
C
)A.$\alpha+\beta$
B.$\alpha-\beta$
C.$\beta-\alpha$
D.$\alpha$
答案:
1. C 如图,可知山顶的仰角为$\beta - \alpha$.

1. C 如图,可知山顶的仰角为$\beta - \alpha$.

2. 某观赏渔场有三个观赏亭,观赏亭 $B$ 位于观赏亭 $A$ 的东北方向且它们之间的距离为 $10\ m$,观赏亭 $B$ 位于观赏亭 $C$ 的北偏西 $15^{\circ}$ 方向且它们之间的距离为 $20\ m$,则观赏亭 $A$ 与观赏亭 $C$ 之间的距离为(
A.$10\ m$
B.$10\sqrt{2}\ m$
C.$10\sqrt{3}\ m$
D.$20\ m$
C
)A.$10\ m$
B.$10\sqrt{2}\ m$
C.$10\sqrt{3}\ m$
D.$20\ m$
答案:
2. C 如图,由题意知$AB = 10$,$BC = 20$,$\angle ABC = 45^{\circ}+15^{\circ}=60^{\circ}$.在$\triangle ABC$中,由余弦定理,可得$AC=\sqrt{AB^{2}+BC^{2}-2AB· BC\cos\angle ABC}=\sqrt{100 + 400 - 2×10×20×\frac{1}{2}}=10\sqrt{3}$,即观赏亭$A$与观赏亭$C$之间的距离为$10\sqrt{3} m$.

2. C 如图,由题意知$AB = 10$,$BC = 20$,$\angle ABC = 45^{\circ}+15^{\circ}=60^{\circ}$.在$\triangle ABC$中,由余弦定理,可得$AC=\sqrt{AB^{2}+BC^{2}-2AB· BC\cos\angle ABC}=\sqrt{100 + 400 - 2×10×20×\frac{1}{2}}=10\sqrt{3}$,即观赏亭$A$与观赏亭$C$之间的距离为$10\sqrt{3} m$.

3. 一架高空侦察飞机以 $800\ m/s$ 的速度在海拔 $20000\ m$ 的高空直线飞行,飞机的航线和某个山顶在同一铅垂平面内,飞机第一次探测该山顶的俯角为 $45^{\circ}$,经过 $10\ s$ 后飞机第二次探测该山顶的俯角为 $60^{\circ}$,则该山顶的海拔高度约为(
(参考数据:$\sqrt{2}\approx1.414,\sqrt{3}\approx1.732$)

A.$1072\ m$
B.$1573\ m$
C.$2436\ m$
D.$3200\ m$
(第 3 题)
(第 4 题)
(第 5 题)
A
)(参考数据:$\sqrt{2}\approx1.414,\sqrt{3}\approx1.732$)

A.$1072\ m$
B.$1573\ m$
C.$2436\ m$
D.$3200\ m$
(第 3 题)
(第 4 题)
(第 5 题)
答案:
3. A 如图,设第一次探测点为$A$,第二次探测点为$B$,山顶为点$C$,山高为$h$,过$C$作$CD\perp AB$于$D$.由题意可得$AB = 800×10 = 8000(m)$,又$\tan45^{\circ}=\frac{CD}{AD}$,则$CD = AD = 8000 + BD$,因为$\tan60^{\circ}=\frac{CD}{BD}$,所以$\frac{8000 + BD}{BD}=\sqrt{3}$,解得$BD=\frac{8000}{\sqrt{3}-1}$,所以$CD=\frac{8000\sqrt{3}}{\sqrt{3}-1}$,故$h = 20000-\frac{8000\sqrt{3}}{\sqrt{3}-1}=20000 - 4000×(3 + \sqrt{3})\approx1072(m)$.

3. A 如图,设第一次探测点为$A$,第二次探测点为$B$,山顶为点$C$,山高为$h$,过$C$作$CD\perp AB$于$D$.由题意可得$AB = 800×10 = 8000(m)$,又$\tan45^{\circ}=\frac{CD}{AD}$,则$CD = AD = 8000 + BD$,因为$\tan60^{\circ}=\frac{CD}{BD}$,所以$\frac{8000 + BD}{BD}=\sqrt{3}$,解得$BD=\frac{8000}{\sqrt{3}-1}$,所以$CD=\frac{8000\sqrt{3}}{\sqrt{3}-1}$,故$h = 20000-\frac{8000\sqrt{3}}{\sqrt{3}-1}=20000 - 4000×(3 + \sqrt{3})\approx1072(m)$.

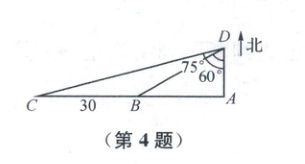
4. 如图,一艘船 $A$ 向正北航行,看见正西方向有相距 $30\ n mile$ 的 $B,C$ 两个灯塔恰好与它在一条直线上,继续航行 $1\ h$ 后,看见灯塔 $B$ 在船的南偏西 $60^{\circ}$ 方向,灯塔 $C$ 在船的南偏西 $75^{\circ}$ 方向,则这艘船的速度是(
A.$15\ n mile/h$
B.$15\sqrt{3}\ n mile/h$
C.$30\ n mile/h$
D.$30\sqrt{3}\ n mile/h$
A
)
A.$15\ n mile/h$
B.$15\sqrt{3}\ n mile/h$
C.$30\ n mile/h$
D.$30\sqrt{3}\ n mile/h$
答案:
4. A 设船的速度为$a n mile/h$,则由图易知$AB=\sqrt{3}a$,$AC=a·\tan75^{\circ}=(2 + \sqrt{3})a$,$BC = AC - AB = 2a$,又$BC = 30$,所以$a = 15$.
5. 古代数学家刘徽编撰的《重差》是中国最早的一部测量学著作,也为地图学提供了数学基础,根据刘徽的《重差》测量一个球体建筑的高度,已知点 $A$ 是球体建筑物与水平地面的接触点(切点),地面上 $B,C$ 两点与点 $A$ 在同一条直线上,且在点 $A$ 的同侧,若在 $B,C$ 处分别测量球体建筑物的最大仰角为 $60^{\circ}$ 和 $20^{\circ}$,且 $BC = 100\ m$,则该球体建筑物的高度约为(参考数据:$\cos10^{\circ}\approx0.985$)(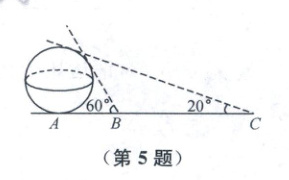
A.$45.25\ m$
B.$50.76\ m$
C.$56.74\ m$
D.$58.60\ m$
B
)
A.$45.25\ m$
B.$50.76\ m$
C.$56.74\ m$
D.$58.60\ m$
答案:
5. B 如图,设球的半径为$R$,则$AB=\frac{R}{\tan30^{\circ}}=\frac{R}{\frac{\sqrt{3}}{3}}=\sqrt{3}R$,$AC=\frac{R}{\tan10^{\circ}}$,所以$BC = AC - AB=\frac{R}{\tan10^{\circ}}-\sqrt{3}R$,又$\cos10^{\circ}\approx0.985$,故$R=\frac{100}{\frac{1}{\tan10^{\circ}}-\sqrt{3}}=\frac{100}{\frac{\cos10^{\circ}}{\sin10^{\circ}}-\sqrt{3}}=\frac{100\sin10^{\circ}}{\cos10^{\circ}-\sqrt{3}\sin10^{\circ}}=2(\frac{\frac{1}{2}\cos10^{\circ}-\frac{\sqrt{3}}{2}\sin10^{\circ}}{\sin10^{\circ}\cos10^{\circ}})=\frac{50\sin10^{\circ}}{2\sin(30^{\circ}-10^{\circ})\cos10^{\circ}}=\frac{50\sin10^{\circ}}{\sin20^{\circ}}\approx\frac{50\sin10^{\circ}}{2\sin10^{\circ}\cos10^{\circ}\cos10^{\circ}}=\frac{25}{\cos10^{\circ}\cos10^{\circ}}\approx\frac{25}{0.985}$,所以$2R=\frac{50}{0.985}\approx50.76$,即该球体建筑物的高度约为$50.76 m$.

5. B 如图,设球的半径为$R$,则$AB=\frac{R}{\tan30^{\circ}}=\frac{R}{\frac{\sqrt{3}}{3}}=\sqrt{3}R$,$AC=\frac{R}{\tan10^{\circ}}$,所以$BC = AC - AB=\frac{R}{\tan10^{\circ}}-\sqrt{3}R$,又$\cos10^{\circ}\approx0.985$,故$R=\frac{100}{\frac{1}{\tan10^{\circ}}-\sqrt{3}}=\frac{100}{\frac{\cos10^{\circ}}{\sin10^{\circ}}-\sqrt{3}}=\frac{100\sin10^{\circ}}{\cos10^{\circ}-\sqrt{3}\sin10^{\circ}}=2(\frac{\frac{1}{2}\cos10^{\circ}-\frac{\sqrt{3}}{2}\sin10^{\circ}}{\sin10^{\circ}\cos10^{\circ}})=\frac{50\sin10^{\circ}}{2\sin(30^{\circ}-10^{\circ})\cos10^{\circ}}=\frac{50\sin10^{\circ}}{\sin20^{\circ}}\approx\frac{50\sin10^{\circ}}{2\sin10^{\circ}\cos10^{\circ}\cos10^{\circ}}=\frac{25}{\cos10^{\circ}\cos10^{\circ}}\approx\frac{25}{0.985}$,所以$2R=\frac{50}{0.985}\approx50.76$,即该球体建筑物的高度约为$50.76 m$.

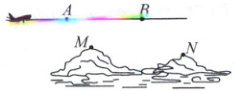
6. 教材变式 如图,为了测量两山顶 $M,N$ 间的距离,飞机沿水平方向飞行,并在 $A,B$ 两点进行测量,$A,B,M,N$ 在同一个铅垂平面内.在点 $A$ 测得 $M,N$ 的俯角分别为 $75^{\circ}$ 和 $30^{\circ}$,在点 $B$ 测得 $M,N$ 的俯角分别为 $45^{\circ}$ 和 $60^{\circ},AB=\sqrt{3}$,则 $MN=$(
A.$\sqrt{3}$
B.$2$
C.$\sqrt{5}$
D.$2\sqrt{2}$
C
)
A.$\sqrt{3}$
B.$2$
C.$\sqrt{5}$
D.$2\sqrt{2}$
答案:
6. C 如图,由题可知,$\angle MAB = 75^{\circ}$,$\angle NAB = 30^{\circ}$,$\angle MBA = 45^{\circ}$,$\angle NBA = 180^{\circ}-60^{\circ}=120^{\circ}$.在$\triangle ABM$中,易得$\angle AMB = 60^{\circ}$,由正弦定理得$\frac{AM}{\sin\angle ABM}=\frac{AB}{\sin\angle AMB}$,所以$AM=\frac{AB·\sin\angle ABM}{\sin\angle AMB}=\frac{\sqrt{3}×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}=\sqrt{2}$.因为$\angle NAB = 30^{\circ}$,$\angle ABN = 120^{\circ}$,则$\angle ANB = 30^{\circ}$,所以$AB = BN = \sqrt{3}$.在$\triangle ABN$中,由余弦定理得$AN^{2}=AB^{2}+BN^{2}-2AB· BN\cos\angle ABC = 3 + 3 + 3 = 9$,则$AN = 3$.因为$\angle MAB = 75^{\circ}$,$\angle NAB = 30^{\circ}$,所以$\angle MAN = 45^{\circ}$.在$\triangle AMN$中,由余弦定理得$MN^{2}=AM^{2}+AN^{2}-2AM· AN·\cos\angle MAN = 2 + 9 - 6 = 5$,所以$MN=\sqrt{5}$.

6. C 如图,由题可知,$\angle MAB = 75^{\circ}$,$\angle NAB = 30^{\circ}$,$\angle MBA = 45^{\circ}$,$\angle NBA = 180^{\circ}-60^{\circ}=120^{\circ}$.在$\triangle ABM$中,易得$\angle AMB = 60^{\circ}$,由正弦定理得$\frac{AM}{\sin\angle ABM}=\frac{AB}{\sin\angle AMB}$,所以$AM=\frac{AB·\sin\angle ABM}{\sin\angle AMB}=\frac{\sqrt{3}×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}=\sqrt{2}$.因为$\angle NAB = 30^{\circ}$,$\angle ABN = 120^{\circ}$,则$\angle ANB = 30^{\circ}$,所以$AB = BN = \sqrt{3}$.在$\triangle ABN$中,由余弦定理得$AN^{2}=AB^{2}+BN^{2}-2AB· BN\cos\angle ABC = 3 + 3 + 3 = 9$,则$AN = 3$.因为$\angle MAB = 75^{\circ}$,$\angle NAB = 30^{\circ}$,所以$\angle MAN = 45^{\circ}$.在$\triangle AMN$中,由余弦定理得$MN^{2}=AM^{2}+AN^{2}-2AM· AN·\cos\angle MAN = 2 + 9 - 6 = 5$,所以$MN=\sqrt{5}$.

查看更多完整答案,请扫码查看


