《2025年小题狂做高中数学必修第二册人教版》

1. 如图是一个直径为12 cm的球形容器和一个底面直径为6 cm、深8 cm的圆柱形水杯(壁厚均不计),则球形容器装满时,约可以倒满水杯(B)

A.3杯
B.4杯
C.5杯
D.6杯

答案： 1. B 球形容器的体积$V_1=\frac{4}{3} \pi × 6^3=288 \pi (cm^3)$，圆柱形水杯的体积$V_2= \pi × 3^2 × 8=72 \pi (cm^3)$，所以$V_1=4V_2$，则球形容器装满时，约可以倒满水杯 4 杯.

2. 教材变式 已知圆锥的表面积为8π,且它的侧面展开图是一个圆心角为$\frac {2π}{3}$的扇形,则这个圆锥的体积为(C)

A.$\frac {5π}{3}$
B.2π
C.$\frac {8π}{3}$
D.3π

答案： 2. C 设圆锥的母线为$l$，底面半径为$r$，高为$h$，则$\frac{2 \pi r}{l}= \frac{2 \pi}{3}$，得$l=3r$.又圆锥的表面积为$S= \pi rl+ \pi r^2=4 \pi r^2=8 \pi$，解得$r^2=2$，即$r= \sqrt{2}$，所以$h= \sqrt{l^2-r^2}=2 \sqrt{2}r=4$，所以圆锥的体积为$V= \frac{1}{3} \pi r^2h= \frac{1}{3} \pi × 2 × 4= \frac{8 \pi}{3}$.
教材链接 人教 A 版必修二 8.3.2 练习第 1 题改编

3. 一圆台的上、下底面半径分别为2,4,体积为$\frac {56\sqrt {3}}{3}π$,则该圆台的侧面积为(C)

A.12π
B.18π
C.24π
D.36π

答案： 3. C 根据题意可知，圆台上底面面积为$S_1=4 \pi$，下底面面积为$S_2=16 \pi$.设圆台的高为$h$，则$\frac{1}{3}h(S_1+S_2+ \sqrt{S_1S_2})= \frac{1}{3} × (4 \pi+16 \pi+8 \pi)h= \frac{56 \sqrt{3}}{3} \pi$，解得$h=2 \sqrt{3}$，所以圆台的母线长为$l= \sqrt{(2 \sqrt{3})^2+(4-2)^2}=4$，故圆台的侧面积为$ \pi × (2+4) × 4=24 \pi$.

4. 若轴截面为正方形的圆柱内接于半径为1的球,则该圆柱的体积为(B)

A.$\sqrt {2}π$
B.$\frac {\sqrt {2}π}{2}$
C.$\frac {\sqrt {2}π}{4}$
D.$\frac {\sqrt {2}π}{6}$

答案：
4. B 如图，由题意知，$OA \perp OB$，则圆柱的高为$h= \sqrt{OA^2+OB^2}= \sqrt{2}$，底面圆的半径为$r= \frac{ \sqrt{OA^2+OB^2}}{2}= \frac{ \sqrt{2}}{2}$，则圆柱的体积$V= \pi r^2h= \frac{ \sqrt{2} \pi}{2}$.

5. 已知球O的半径R为2,一母线长与圆锥底面直径相等的圆锥位于球内,圆锥顶点在球面上,底面与球面相接,则该圆锥的体积为(C)

A.$3\sqrt {3}π$
B.$3\sqrt {2}π$
C.3π
D.$2\sqrt {2}π$

答案：
5. C 如图，设圆锥的底面半径为$r$，由题意知圆锥轴截面为正三角形，则圆锥的高为$\sqrt{3}r$，得$(\sqrt{3}r-R)^2+r^2=R^2$，即$(\sqrt{3}r-2)^2+r^2=2^2$，解得$r=\sqrt{3}$，则圆锥的体积为$\frac{1}{3} \pi × (\sqrt{3})^2 × 3=3 \pi$.

方法总结 几个与球有关的切、接的常用结论
(1)正方体的棱长为$a$，球的半径为$R$，①若球为正方体的外接球，则$2R= \sqrt{3}a$；②若球为正方体的内切球，则$2R=a$；③若球与正方体的各棱相切，则$2R= \sqrt{2}a$.
(2)若长方体的同一顶点的三条棱长分别为$a$，$b$，$c$，外接球的半径为$R$，则$2R= \sqrt{a^2+b^2+c^2}$.
(3)对于正棱锥，其外接球的球心在底面多边形外接圆的圆心与正棱锥顶点的连线上，球的半径、底面所在截面圆的半径、截面圆的圆心到球心的距离满足勾股定理；因其内切球与各个面相切，内切球半径的大小可以通过等体积法求得.
(4)对于直棱柱，其外接球的球心在两底面多边形外接圆圆心的连线上，球的半径、底面所在截面圆的半径、直棱柱的高的一半满足勾股定理.

6. 魏晋时期数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成几何体为“牟合方盖”，刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为$π:4$,若“牟合方盖”的体积为18,则正方体的棱长为(C)

A.18
B.6
C.3
D.2

答案： 6. C 因为“牟合方盖”的体积为 18，所以该正方体的内切球的体积为$18 × \frac{ \pi}{4}= \frac{9 \pi}{2}$.设正方体的棱长为$a$，则该正方体的内切球半径为$\frac{a}{2}$，所以$\frac{4}{3} \pi × (\frac{a}{2})^3= \frac{9 \pi}{2}$，解得$a=3$.

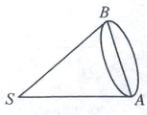
7. 如图是底面半径为2的圆锥,将其放倒在一平面上,使圆锥在此平面内绕顶点S逆时针滚动,当这个圆锥转回原位置时,圆锥本身恰好滚动了3周,则下列结论正确的是(BC)

A.圆锥的母线长为12
B.圆锥的侧面积为12π
C.圆锥的侧面展开图扇形圆心角为$\frac {2π}{3}$
D.圆锥的体积为$16\sqrt {2}π$

答案： 7. BC 设圆锥的母线长为$l$，则以$S$为圆心，$SA$为半径的圆的面积为$S= \pi l^2$，又圆锥的侧面积$S_{圆锥侧}= \pi rl=2 \pi l$，因为圆锥在平面内转到原位置时，圆锥本身滚动了 3 周，所以$ \pi l^2=3 × 2 \pi l$，解得$l=6$，故 A 错误；圆锥的侧面积$S_{圆锥侧}=2 × \pi × 6=12 \pi$，故 B 正确；因为圆锥的底面周长为$2 \pi × 2=4 \pi$，设圆锥的侧面展开图扇形圆心角为$ \alpha$，则$4 \pi= \alpha · 6$，解得$ \alpha= \frac{2 \pi}{3}$，故 C 正确；圆锥的高$h= \sqrt{l^2-r^2}= \sqrt{36-4}=4 \sqrt{2}$，所以圆锥的体积为$V= \frac{1}{3} × \pi × 2^2 × 4 \sqrt{2}= \frac{16 \sqrt{2} \pi}{3}$，故 D 错误.

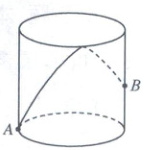
8. 如图,底面半径为1,高为2的圆柱简,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱简表面,由A点经过圆柱简的上底面爬到内壁(圆柱简的厚度忽略不计)上的B点,其中B为高的中点,则蚂蚁爬行的距离可能为(CD)


A.3
B.4
C.5
D.6

答案：
8. CD 如图，沿母线将圆柱侧面展开，为一个矩形，长为$2 \pi$，宽为 2，设$B$关于矩形上底边的对称点为$B_1$，则蚂蚁爬行的最短距离为$AB_1= \sqrt{ \pi^2+9}$.因为$ \sqrt{ \pi^2+9} \in (3 \sqrt{2},5)$，所以蚂蚁爬行的距离可能为 C,D.