《2025年小题狂做高中数学选择性必修第二册人教版》

1. 已知数列 $ 1,-\sqrt{2},\sqrt{3},-2,\sqrt{5},·s $,则该数列的第36项为（ ）

A.$-36$
B.$36$
C.$-6$
D.$6$

答案： 1. C 由数列$1,-\sqrt{2},\sqrt{3},-2,\sqrt{5},·s$，即$\sqrt{1},-\sqrt{2},\sqrt{3},-\sqrt{4},\sqrt{5},·s$，归纳可得该数列的通项公式为$a_{n}=(-1)^{n + 1}\sqrt{n}$，所以$a_{36}=(-1)^{36 + 1}\sqrt{36}=-6$。
解题突破 摆动数列通项公式的求法
分奇数、偶数的摆动数列，我们往往逐一写出前面有限项，并观察其规律.

2. 在数列 $ 1,1,2,3,5,8,x,21,34,55,·s $中,$x=$（ ）

A.$11$
B.$12$
C.$13$
D.$14$

答案： 2. C 设该数列为$\{a_{n}\}$，则$a_{n}=a_{n - 1}+a_{n - 2}(n\geq3)$，所以$x = a_{7}=a_{5}+a_{6}=5 + 8 = 13$。

3. 已知数列 $ 1,-1,2,-2,3,-3,·s $,根据该数列的规律,100是该数列的第（ ）

A.100项
B.101项
C.199项
D.200项

答案： 3. C 根据该数列的规律可将数列进行分组，每一组中两项互为相反数，因此$100$即为第$100$组的第一个数，其前面有$99$组，每一组有两项.所以$100$是该数列的第$2×99 + 1 = 199$项.

4. 已知 $ a_{n}=-2n^{2}+25n+30 $,则数列$\{ a_{n}\}$中最大项的值是（ ）

A.$107$
B.$108$
C.$108\frac{1}{8}$
D.$109$

答案： 4. B 由题意可知$a_{n}=-2n^{2}+25n + 30=-2(n-\frac{25}{4})^{2}+108\frac{1}{8}$.由于$n\in N^{*}$，故当$n$取距离$\frac{25}{4}$最近的正整数$6$时，$a_{n}$取得最大值$108$，即数列$\{a_{n}\}$中的最大项为$a_{6}=108$。

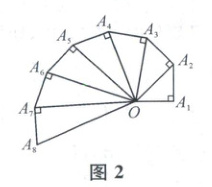
5. 如图1是第七届国际数学教育大会(简称ICME-7)的会徽图案,会徽的主体图案是由如图2所示的一连串直角三角形演化而成的,其中 $ OA_{1}=A_{1}A_{2}=A_{2}A_{3}=·s =A_{7}A_{8}=1 $.若把图2中的直角三角形继续作下去,记 $ OA_{1},OA_{2},·s,OA_{n},·s $的长度构成数列$\{ a_{n}\}$,则此数列的通项公式为（ ）

A.$ a_{n}=n $
B.$ a_{n}=\sqrt{n + 1} $
C.$ a_{n}=\sqrt{n} $
D.$ a_{n}=n^{2} $

答案： 5. C 因为$OA_{1}=1,OA_{2}=\sqrt{2},OA_{3}=\sqrt{3},·s,OA_{n}=\sqrt{n}$，所以$a_{1}=1,a_{2}=\sqrt{2},·s,a_{n}=\sqrt{n}$。

6. 已知数列$\{ a_{n}\}$是递增数列,且其通项公式为 $ a_{n}=n^{2}+\lambda n $,则实数$\lambda$的取值范围是（ ）

A.$ \left(-\frac{7}{2},+\infty\right) $
B.$ [0,+\infty) $
C.$ [-2,+\infty) $
D.$ (-3,+\infty) $

答案： 6. D 解法1 由$\{a_{n}\}$是递增数列且$a_{n}=n^{2}+\lambda n$，得$a_{n + 1}-a_{n}=(n + 1)^{2}+\lambda(n + 1)-(n^{2}+\lambda n)=2n + 1+\lambda＞0$对$n\in N^{*}$恒成立，所以$\lambda＞[- (2n + 1)]_{\max}$，即$\lambda＞-3$。
解法2 由$\{a_{n}\}$递增得$-\frac{\lambda}{2}＜\frac{3}{2}$，得$\lambda＞-3$。
易错警示 用函数的单调性研究数列的单调性的注意点
如果转化为二次函数在$(1,+\infty)$上单调递增，则$-\frac{\lambda}{2}＜1$，即$\lambda＞-2$，此法错误，错误的原因在于只要满足$a_{1}＜a_{2}$，没必要保证在$(1,+\infty)$上单调递增.