《2025年小题狂做高中数学必修第二册人教版》

8. 已知 $ \triangle ABC $ 外接圆的圆心为 $ O $,半径为 2,且 $ \overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}=\boldsymbol{0} $,$ |\overrightarrow{OA}|=|\overrightarrow{AB}| $,则 (ACD)

A.$ \overrightarrow{OC} $ 与 $ \overrightarrow{AB} $ 共线
B.$ \langle\overrightarrow{OC},\overrightarrow{CA}\rangle=\frac{\pi}{2} $
C.$ \overrightarrow{OA} \perp \overrightarrow{BC} $
D.$ \overrightarrow{CA} $ 在 $ \overrightarrow{CB} $ 上的投影向量的长度为 $ \sqrt{3} $

答案：
8.ACD因为OA+AB+AC=0，所以OA+OB−OA+OC−OA=0，所以OC=OA−OB=BA=−AB，故A正确；因为OC=BA，所以四边形OBAC为平行四边形，如图：又O为△ABC外接圆的圆心，所以|OB|=|OA|，又|OA|=|AB|，所以△OAB为正三角形，因为△ABC外接圆的半径为2，所以四边形OBAC是边长为2的菱形，所以∠OCA=π/3，⟨OC,CA⟩=π−π/3=2π/3，故B错误；由以上分析知四边形OBAC是边长为2的菱形，所以OA⊥BC，故C正确；由四边形OBAC是边长为2的菱形，可得∠ACB=π/6，所以CA在CB上的投影向量的长度为|CA|cos(π/6)=2×(√3/2)=√3，故D正确.

9. 在正方形 $ ABCD $ 中,$ BC = 1 $,点 $ E $ 满足 $ \overrightarrow{DE}=t\overrightarrow{DC}(0 ＜ t ＜ 1) $,则下列说法正确的是 (AD)

A.当 $ t=\frac{1}{3} $ 时,$ \overrightarrow{AE}=\frac{1}{3}\overrightarrow{AB}+\overrightarrow{AD} $
B.当 $ t=\frac{2}{3} $ 时,$ \cos\langle\overrightarrow{AE},\overrightarrow{BE}\rangle=\frac{\sqrt{35}}{10} $
C.存在 $ t $,使得 $ \overrightarrow{AE} \perp \overrightarrow{BE} $
D.$ |\overrightarrow{AE}+\overrightarrow{BE}| $ 的最小值为 2

答案：
9.AD以A为原点，AB,AD所在直线分别为x轴和y轴，建立如图所示的平面直角坐标系，则A(0,0),B(1,0),C(1,1)，D(0,1)，故AB=(1,0),AD=(0,1).对于A，当t=1/3时，由DE=tDC(0＜t＜1)，可知E(1/3,1)，所以AE=(1/3,1)，又AD+1/3AB=(0,1)+1/3(1,0)=(1/3,1)，故AE=1/3AB+AD，故A正确；对于B，当t=2/3时，由DE=tDC(0＜t＜1)，可知E(2/3,1)，所以AE=(2/3,1)，BE=(2/3−1,1−0)=(−1/3,1)，所以cos⟨AE,BE⟩=(AE·BE)/(|AE||BE|)=((2/3)×(−1/3)+1×1)/(√((2/3)²+1²)√((−1/3)²+1²))=7√130/130，故B错误；对于C，由DE=tDC(0＜t＜1)可得E(t,1)，故AE=(t,1)，BE=(t−1,1−0)=(t−1,1)，则AE·BE=(t,1)·(t−1,1)=t(t−1)+1×1=t²−t+1=(t−1/2)²+3/4＞0，故不存在t，使得AE⊥BE，故C错误；对于D，由C得AE+BE=(t,1)+(t−1,1)=(2t−1,2)，故|AE+BE|=√((2t−1)²+2²)=√(4(t−1/2)²+4)，又0＜t＜1，故当t=1/2时，|AE+BE|取得最小值为√4=2，故D正确.

10. 在平面四边形 $ ABCD $ 中,$ A(0,0) $,$ B(-3,1) $,$ C(-2,3) $,$ D(3,5) $,则该四边形的面积为13.

答案： 10.13因为AC=(−2,3),BD=(6,4)，所以AC·BD=−12+12=0，则AC⊥BD，所以四边形ABCD面积为1/2|AC|·|BD|=1/2×√(4+9)×√(36+16)=13.

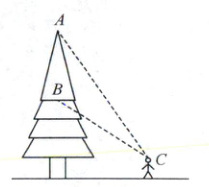
11. 如图,已知树顶 $ A $ 离地面 $ \frac{21}{2} $ m,树上另一点 $ B $ 离地面 $ \frac{11}{2} $ m,某人在离地面 $ \frac{3}{2} $ m 的 $ C $ 处看此树,则该人看 $ A $, $ B $ 两点的视角最大时,离此树的距离为6 m.

答案：
11.6建立如图所示的平面直角坐标系，则A(0,21/2),B(0,11/2)，设C(x,3/2)(x＞0)，则CA=(−x,9),CB=(−x,4)，所以cos∠ACB=(CA·CB)/(|CA|·|CB|)=(x²+36)/(√(x²+81)·√(x²+16))=1/√(((x²+81)(x²+16))/((x²+36)²))=1/√(1+(25x²+36×16)/((x²+36)²)).令1/(x²+36)=t，则cos∠ACB=1/√(1+25t−900t²)，所以当t=1/72时，cos∠ACB取最小值，又0＜∠ACB＜π，且余弦函数在(0,π)上单调递减，所以当1/(x²+36)=1/72，即x=6时，∠ACB最大，即该人距离此树6m时，看A,B两点的视角最大.

12. 在边长为 6 的正方形 $ ABCD $ 中,$ E $, $ F $ 分别为边 $ AD $, $ DC $ 上的点,且满足 $ \frac{AE}{ED}=\frac{CF}{FD}=2 $, $ G $ 是正方形 $ ABCD $ 边上的任意一点,则 $ \overrightarrow{GE} · \overrightarrow{GF} $ 的最大值为48.

答案： 12.48连接EF，取EF的中点O，连接GO，由题意知DE=DF=2，所以EF=2√2，则GE·GF=(GO+OE)·(GO+OF)=(GO+OE)·(GO−OE)=GO²−OE²=|GO|²−2.易知当点G与点B重合时，|GO|取得最大值，故由正方形的性质知|GO|max=5/6|BD|=5/6×6√2=5√2，所以GE·GF的最大值为(5√2)²−2=48.

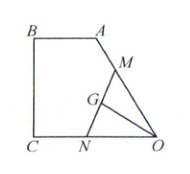
13. 如图所示,已知直角梯形 $ ABCO $ 中,$ \angle ABC=\angle BCO = 90^{\circ} $,$ AB = 1 $,$ BC=\sqrt{3} $,$ OA = OC = 2 $. 设 $ \overrightarrow{OM}=m\overrightarrow{OA} $,$ \overrightarrow{ON}=n\overrightarrow{OC} $(其中 $ 0 ＜ m,n ＜ 1 $), $ G $ 为线段 $ MN $ 的中点.
(1)当 $ m=\frac{1}{2} $ 时,$ O $, $ G $, $ B $ 三点共线,求 $ n $ 的值;
(2)若 $ \triangle OMN $ 的面积为 $ \frac{\sqrt{3}}{4} $,求 $ |\overrightarrow{OG}| $ 的最小值.

答案：
13.解法1
(1)依题意，OB=OA+AB=OA+1/2OC，OG=1/2(OM+ON)=1/2(1/2OA+nOC)=1/4OA+n/2OC，因为O,G,B三点共线，所以OG=λOB，即1/4OA+n/2OC=λ(OA+1/2OC)，所以{1/4=λ, n/2=λ/2,}解得n=1/4.
(2)由平面几何知识易得∠AOC=60°，在△OMN中，边OM上的高为|ON|sin∠AOC，所以S△OMN=1/2|OM|·|ON|sin∠AOC=√3mn=√3/4，所以mn=1/4.OG=1/2(OM+ON)=1/2(mOA+nOC)，所以|OG|²=1/4(m²OA²+n²OC²+2mnOA·OC)=1/4(4m²+4n²+4mn)=m²+n²+mn≥3mn=3/4，当且仅当m=n=1/2时等号成立，所以|OG|的最小值为√3/2. 解法2建立平面直角坐标系如图所示，依题意得O(2,0)，B(0,√3),A(1,√3)，由OM=mOA,ON=nOC，得M(2−m,√3m),N(2−2n,0)，则G(2−m/2−n,√3m/2).
(1)当m=1/2时，G(7/4−n,√3/4)，则OG=(−1/4−n,√3/4),OB=(−2,√3)，由O,G,B三点共线，则−√3/4−√3n=−√3/2，解得n=1/4.
(2)因为S△OMN=1/2|ON|·|yM|=1/2·2n·√3m=√3/4，所以mn=1/4，则|OG|=√((m/2+n)²+3/4m²)=√(m²+n²+mn)≥√(3mn)=√3/2，当且仅当m=n=1/2时等号成立，所以|OG|的最小值为√3/2.