《2026年练就优等生课后提分攻略八年级数学全一册人教版》

01 1876年,美国总统伽菲尔德利用如图5-58-1所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是(B)

A.$ S_{△EDA}=S_{△CEB} $
B.$ S_{△EDA}+S_{△CDE}+S_{△CEB}=S_{四边形ABCD} $
C.$ S_{△EDA}+S_{△CEB}=S_{△CDE} $
D.$ S_{四边形AECD}=S_{四边形DEBC} $

答案： 01 B

02 我国著名的数学家赵爽,早在公元3世纪,就把一个矩形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图5-58-2①),这个正方形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中,两直角边a,b与斜边c满足关系式$ a^{2}+b^{2}=c^{2} $,此关系式被称为勾股定理.
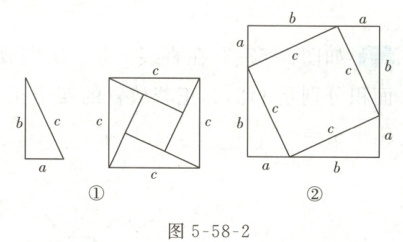
爱动脑筋的小明把这四个全等的直角三角形拼成了另一个更大的正方形(如图5-58-2②),也能验证这个结论,请你帮助小明完成验证的过程.

答案： 证明：大正方形面积=$4 × \frac {1}{2}ab + c ^ {2} = (a + b) ^ {2}$，整理，得$2ab + c ^ {2} = a ^ {2} + b ^ {2} + 2ab$，
$\therefore c ^ {2} = a ^ {2} + b ^ {2}$，
即直角三角形两直角边的平方和等于斜边的平方。

03 探索与研究:
(1)如图5-58-3①,对任意的直角三角形ABC绕其锐角顶点A逆时针旋转$ 90^{\circ} $,得到$ ∠BAE=90^{\circ} $,且四边形ACFD是一个正方形,它的面积和四边形ABFE的面积相等,而四边形ABFE的面积等于$ Rt△BAE $和$ Rt△BFE $的面积之和.根据图示写出勾股定理的证明过程.
(2)任意两个全等的$ Rt△BEA $和$ Rt△ACD $拼成的图形如图5-58-3②所示,你能根据图示再写出一种证明勾股定理的方法吗?

答案： 解：
(1)证明：由图可得正方形ACFD的面积等于四边形ABFE的面积等于Rt△BAE和Rt△BFE的面积之和，即$S_{正方形ACFD}=S_{△BAE}+S_{△BFE}$，
$\therefore b ^ {2} = \frac {1}{2} c ^ {2} + \frac {(b + a)(b - a)}{2}$
整理，得$a ^ {2} + b ^ {2} = c ^ {2}$.
(2)此图也可以看成Rt△BEA绕其直角顶点顺时针旋转$90 ^ { \circ }$，再向下平移得到，则$\angle BAD = 90 ^ { \circ }$.一方面，四边形ABCD的面积等于△ABC和Rt△ACD的面积之和；另一方面，四边形ABCD的面积等于Rt△ABD和△BCD的面积之和，
$\therefore S_{△ABC} + S_{△ACD} = S_{△ABD} + S_{△BCD}$，
即$\frac {1}{2} b ^ {2} + \frac {1}{2} ab = \frac {1}{2} c ^ {2} + \frac {1}{2} a(b - a)$，
整理，得$b ^ {2} + ab = c ^ {2} + a(b - a)$，
$\therefore a ^ {2} + b ^ {2} = c ^ {2}$.