《2026年练就优等生课后提分攻略八年级数学全一册人教版》

如图 1 - 13 - 1，已知 C 是∠MAN 的平分线上一点，∠BCD 的两边 CB，CD 分别与射线 AM，AN 相交于 B，D 两点，且∠ABC + ∠ADC = 180°。过点 C 作 CE⊥AB，垂足为 E.
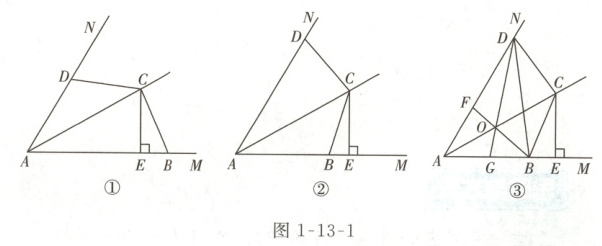
(1)如图①，当点 E 在线段 AB 上时，求证：BC = DC.
(2)如图②，当点 E 在线段 AB 的延长线上时，探究线段 AB，AD 与 BE 之间的数量关系.
(3)如图③，在(2)的条件下，若∠MAN = 60°，连接 BD，作∠ABD 的平分线 BF 交 AD 于点 F，交 AC 于点 O，连接 DO 并延长交 AB 于点 G. 若 BG = 1，DF = 2，求线段 DB 的长.

答案：
题组013　　角的轴对称性之“垂两边”模型
解:
(1)证明:如图①,过点C作CF⊥AD,垂足为F.
　　　　　　　　　
∵AC平分∠MAN,CE⊥AB,CF⊥AD,
∴CE=CF.
∵∠CBE+∠ADC=180°,∠CDF+∠ADC=180°,
∴∠CBE=∠CDF.
在△BCE和△DCF中，
　∠CBE=∠CDF,
　∠CEB=∠CFD=90°,
　CE=CF,
∴△BCE≌△DCF(AAS).
∴BC=DC.
(2)AD - AB = 2BE. 理由如下:如图②，过点C作CF⊥AD,垂足为F.
　　　　　　　　　
∵AC平分∠MAN,CE⊥AB,CF⊥AD,
∴CE=CF,AE=AF.
∵∠ABC+∠ADC=180°,∠ABC+∠CBE=180°,
∴∠CDF=∠CBE.
在△BCE和△DCF中，
　∠CBE=∠CDF,
　∠CEB=∠CFD=90°,
　CE=CF,
∴△BCE≌△DCF(AAS).
∴BE=DF.
∴AD=AF+DF=AB+BE+DF=AB+2BE.
∴AD - AB = 2BE.
(3)如图③,在BD上截取BH=BG,连接OH.
　　　　　　　　　
在△OBH和△OBG中，
　BH=BG,
　∠OBH=∠OBG,
　OB=OB,
∴△OBH≌△OBG(SAS).
∴∠BOH=∠BOG,∠OHB=∠OGB.
∵AO是∠MAN的平分线，BO是∠ABD的平分线，
∴点O到AD,AB,BD的距离相等.
∴∠ODH=∠ODF.
∵∠OHB=∠ODH+∠DOH,∠OGB=∠ODF+∠DAB,
∴∠DOH=∠DAB=60°.
∴∠GOH=120°.
∴∠BOG=∠BOH=60°.
∴∠DOF=∠BOG=60°.
∴∠DOH=∠DOF.
在△ODH和△ODF中，
　∠DOH=∠DOF,
　OD=OD,
　∠ODH=∠ODF,
∴△ODH≌△ODF(ASA).
∴DH=DF.
∴DB=DH+BH=DF+BG=2 + 1 = 3.
008练就优等生初中数学八年级(RJ)8练就优等生初中数学八年级(RJ)