《2026年练就优等生课后提分攻略八年级数学全一册人教版》

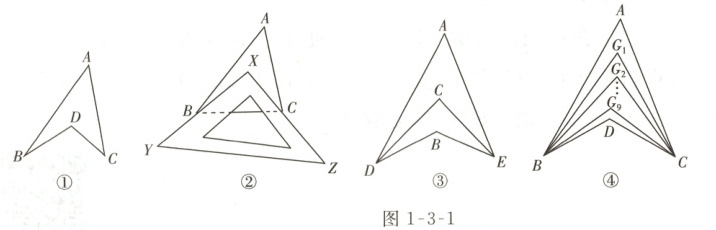
如图 1 - 3 - 1①所示的图形像我们常见的风筝，我们不妨把这样的图形叫做“筝形”。在这样一个简单的图形中，隐藏了哪些数学知识呢？下面就请发挥你的聪明才智，解决下列问题：
(1)观察“筝形”，试探究$∠BDC$与$∠A$，$∠B$，$∠C$之间的数量关系，并说明理由。
(2)请你直接利用(1)中的结论，解决以下问题：
①如图 1 - 3 - 1②，把一块三角尺$XYZ$放置在$△ABC$上，使三角尺的两条直角边$XY$，$XZ$分别经过点$B$，$C$。若$∠A = 50^{\circ}$，则$∠ABX + ∠ACX =$40°。
②如图 1 - 3 - 1③，$DC$平分$∠ADB$，$EC$平分$∠AEB$，若$∠DAE = 50^{\circ}$，$∠DBE = 130^{\circ}$，求$∠DCE$的度数。
③如图 1 - 3 - 1④，$∠ABD$，$∠ACD$的 10 等分线分别相交于点$G_{1}$，$G_{2}$，$·s$，$G_{9}$，若$∠BDC = 140^{\circ}$，$∠BG_{1}C = 77^{\circ}$，求$∠A$的度数。

答案：
解:
(1)∠BDC = ∠BAC + ∠B + ∠C.理由如下:如图，连接AD并延长至点F.

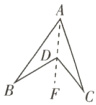
由三角形外角的性质可得∠BDF = ∠BAD + ∠B，∠CDF = ∠C + ∠CAD，且∠BDC = ∠BDF + ∠CDF，∠BAC = ∠BAD + ∠CAD，
∴∠BDC = ∠BAC + ∠B + ∠C.
(2)①40°
②由
(1)的结论易得∠DCE = ∠A + ∠ADC + ∠AEC，∠DBE = ∠A + ∠ADB + ∠AEB，
∴∠ADB + ∠AEB = 130° - 50° = 80°.
∵DC平分∠ADB，EC平分∠AEB，
∴∠ADC = $\frac{1}{2}$∠ADB，∠AEC = $\frac{1}{2}$∠AEB.
∴∠DCE = $\frac{1}{2}$(∠ADB + ∠AEB) + ∠A.
∴∠DCE = 40° + 50° = 90°.
③∠BG₁C = $\frac{1}{10}$(∠ABD + ∠ACD) + ∠A = 77°，
设∠A的度数为x°.
∵∠ABD + ∠ACD = ∠BDC - ∠A = 140° - x°，
∴$\frac{1}{10}$(140 - x) + x = 77，解得x = 70.
∴∠A = 70°.