《2025年大联考单元期末测试卷九年级数学全一册沪科版》

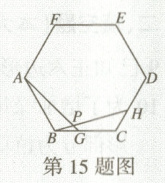
15. 如图,点 $ G $, $ H $ 分别是正六边形 $ ABCDEF $ 的边 $ BC $, $ CD $ 上的点,且 $ BG = CH $, $ AG $ 与 $ BH $ 交于点 $ P $. (1)求证: $ \triangle ABG \cong \triangle BCH $. (2)求 $ \angle APH $ 的度数.

答案： 15.解：
(1)证明：$\because$六边形$ABCDEF$是正六边形，
$\therefore AB = BC$，$\angle ABC = \angle C = 120^{\circ}$。(2分)
在$\triangle ABG$和$\triangle BCH$中，$\begin{cases} AB = BC, \\ \angle ABC = \angle C = 120^{\circ}, \\ BG = CH, \end{cases}$
$\therefore \triangle ABG \cong \triangle BCH(SAS)$。(4分)
(2)由
(1)知，$\triangle ABG \cong \triangle BCH$，
$\therefore \angle BAG = \angle HBC$，(5分)
$\therefore \angle BAP + \angle ABP = \angle HBC + \angle ABP = 120^{\circ}$，
$\therefore \angle BPG = \angle ABG = 120^{\circ}$，
$\therefore \angle APH = \angle BPG = 120^{\circ}$。(8分)

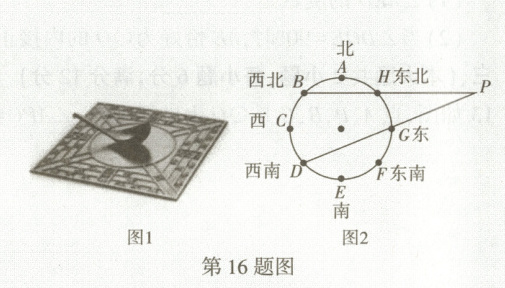
16. 【新情境】司南是我国古代辨别方向用的一种仪器,早在战国时期就已被发明,是现在所用指南 针的始祖(如图 1).司南中心为一圆形,圆心为点 $ O $,直径为 $ 20 \, cm $,根据八个方位将圆形八等分 (图 2 中的点 $ A \sim H $),连接 $ DG $, $ BH $ 并延长交于点 $ P $. (1)点 $ P $ 位于点 $ D $ 的北偏东 $67.5^{\circ}$ 的方向上. (2)求 $ PH $ 的长.

答案：
16.解：
(1)如图，连接$OB$，$OG$，$BD$。
$\because$八个方位将圆形八等分，
$\therefore \angle BOG = 360^{\circ} × \frac{3}{8} = 135^{\circ}$，
$\therefore \angle BDP = \frac{1}{2} \angle BOG = 67.5^{\circ}$，
即点$P$位于点$D$的北偏东$67.5^{\circ}$。
故答案为$67.5^{\circ}$。(3分)

(2)如图，连接$DH$，则$DH$为直径，
$\therefore \angle B = 90^{\circ}$，$DH = 20\ cm$。(5分)
由
(1)知$\angle BDP = 67.5^{\circ}$，
$\therefore \angle P = 90^{\circ} - 67.5^{\circ} = 22.5^{\circ}$。
$\because \angle HOG = 360^{\circ} × \frac{1}{8} = 45^{\circ}$，$\therefore \angle HDG = \frac{1}{2} × 45^{\circ} = 22.5^{\circ}$，$\therefore PH = DH = 20\ cm$。(8分)

17. 综合与实践
主题:装饰锥形草帽.
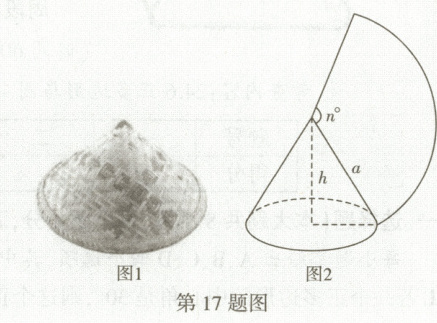
素材:母线长为 $ 25 \, cm $、高为 $ 20 \, cm $ 的锥形草帽(如图 1)和五张颜色不同(红、橙、黄、蓝、紫)、足 够大的卡纸.
步骤 1:将红、橙、黄、蓝、紫卡纸依次按照圆心角 $ 1 : 2 : 1 : 2 : 3 $ 的比例剪成半径为 $ 25 \, cm $ 的 扇形.
步骤 2:将剪下的扇形卡纸依次粘贴在草帽外表面,彩色卡纸恰好覆盖草帽外表面且卡纸连接 处均无缝隙、不重叠,便可得到五彩草帽.
计算与探究:
(1)计算红色扇形卡纸的圆心角的度数.
(2)如图 2,根据(1)的计算过程,直接写出圆锥的高 $ h $、母线长 $ a $ 与侧面展开图的圆心角度数 $ n^{\circ} $ 之间的数量关系:$n = \frac{360\sqrt{a^{2} - h^{2}}}{a}$.

答案： 17.解：
(1)圆锥的底面半径为$\sqrt{25^{2} - 20^{2}} = 15(cm)$。
设侧面展开图的圆心角为$n^{\circ}$，
则$\frac{n\pi × 25}{180} = 2\pi × 15$，解得$n = 216^{\circ}$，
$\therefore 216^{\circ} × \frac{1}{1 + 2 + 1 + 2 + 3} = 24^{\circ}$。
答：红色扇形卡纸的圆心角的度数为$24^{\circ}$。(6分)
(2)$\because$圆锥的底面半径为$\sqrt{a^{2} - h^{2}}$，
$\therefore \frac{n\pi a}{180} = 2\pi \sqrt{a^{2} - h^{2}}$，$\therefore n = \frac{360\sqrt{a^{2} - h^{2}}}{a}$
故答案为$n = \frac{360\sqrt{a^{2} - h^{2}}}{a}$。(10分)