《2025年大联考单元期末测试卷九年级数学全一册沪科版》

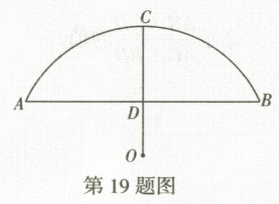
19. 【跨学科·语文】诗句“君到姑苏见,人家尽枕河”所描绘的就是有“东方威尼斯”之称的水城苏州.小勇要帮忙船夫计算一艘货船能否安全通过一座圆弧形的拱桥,现测得桥下水面$AB$宽度为$16m$时,拱顶高出水平面$4m$,货船宽$12m$,船舱顶部为矩形并高出水面$3m$.
(1) 请你帮助小勇求此圆弧形拱桥的半径.
(2) 请你判断一下,此货船能顺利通过这座拱桥吗? 说说你的理由.

答案：
19.解：
(1)如图，连接OB.
∵$OC \perp AB$，
∴点D为AB中点.
∵$AB = 16$m，
∴$BD = \frac{1}{2}AB = 8$m.(2分)
设$OB = OC = r$，则$OD = (r - 4)$m.
在$Rt\triangle BOD$中，根据勾股定理，得$r^2=(r - 4)^2 + 8^2$，解得$r = 10$.
答：此圆弧形拱桥的半径为10m.(5分)

(2)此货船不能顺利通过这座拱桥.理由如下：
如图，连接ON.
∵$CD = 4$m，船舱顶部为矩形并高出水面3m，
∴$CE = 4 - 3 = 1$(m)，
∴$OE = r - CE = 10 - 1 = 9$(m).(7分)
在$Rt\triangle OEN$中，由勾股定理，
得$EN=\sqrt{ON^2 - OE^2}=\sqrt{10^2 - 9^2}=\sqrt{19}$，
∴$MN = 2EN = 2\sqrt{19}＜12$，(9分)
∴此货船不能顺利通过这座拱桥.(10分)

20. 某快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本).若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价$x$(单位:元)取整数,用$y$(单位:元)表示该店日纯收入.该店既要吸引顾客,使每天的销售量较大,又要有较高的日纯收入.按此要求,每份套餐的售价应定为多少元? 此时日纯收入为多少?

答案： 20.解：当$5 ＜ x\leq10$时，该店日纯收入为$y = 400(x - 5)- 600 = 400x - 2600$.(2分)
当$x = 10$时，该店日纯收入为$y = 400x - 2600 = 4000 - 2600 = 1400$.(3分)
当$x ＞ 10$时，该店日纯收入为$y = (x - 5)[400 - 40(x - 10)]- 600 = - 40x^2 + 1000x - 4600$，
∴$y = - 40x^2 + 1000x - 4600 = - 40(x - \frac{25}{2})^2 + 1650$.(6分)
∵售价x取整数，
∴当$x = 12$或$x = 13$时，日销售量最大.(8分)
又
∵要吸引顾客，使每天销售量较大，
∴当售价为12元时，
最大利润为$y = - 40(x - \frac{25}{2})^2 + 1650 = 1640$，
∴每份套餐的售价应定为12元，此时日纯收入为1640元.(10分)