《2025年大联考单元期末测试卷九年级数学全一册沪科版》

18. 【核心素养·抽象能力】通过实验研究发现,初中生在课堂中的专注度随着上课时间的变化而变化,刚上课时,学生兴趣激增,10 min 后保持平稳一段时间,20 min 后注意力开始分散.若学生的专注度 $ y $ 随时间 $ x $(单位:min)变化的函数图象如图所示,当 $ 0 \leq x ＜ 10 $ 和 $ 10 \leq x ＜ a $ 时,图象是线段;当 $ a \leq x \leq 45 $ 时,图象是双曲线的一部分.根据函数图象回答下列问题.
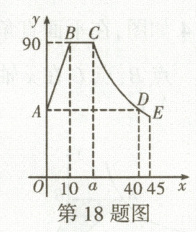
(1) $ a = $20.
(2) 当 $ 0 \leq x ＜ 10 $ 时,求 $ y $ 与 $ x $ 的函数表达式.
(3) 数学老师讲一道函数综合题需要 25 min,他能否经过适当的安排,使学生在听这道题目的讲解时,专注度不低于 60? 请说明理由.

答案： 18.解:
(1)20.(2分)
(2)由
(1)可知,点C的坐标为(20,90).
设双曲线对应的函数表达式为$y=\frac{k}{x}(x＞0).$
将(20,90)代入,得$90=\frac{k}{20},$解得k=1800,
∴双曲线对应的函数表达式为$y=\frac{1800}{x}(x＞$
0).(4分)
将x=40代入$y=\frac{1800}{x},$得$y=\frac{1800}{40}=45,$
∴点D的坐标为(40,45),点A的坐标为(0,45).
由图可得点B的坐标为(10,90),
设当0≤x＜10时,y与x的函数表达式为y=
mx+n.
将(0,45),(10,90)代入,
得$\begin{cases}n=45,\\10m+n=90,\end{cases}$
解得$\begin{cases}m=\frac{9}{2},\\n=45,\end{cases}$
∴y与x的函数表达式为$y=\frac{9}{2}x+45.(6$分)
(3)经过适当的安排,能使学生在听这道题目的讲解时,专注度不低于60.
理由如下:
由题意,当y≥60时,
$\begin{cases}\frac{9}{2}x+45≥60(0≤x$＜10),\\90＞60(10≤x＜20),\frac{1800}{x}≥60(20≤x≤45),\end{cases}
解得$\frac{10}{3}≤x≤30.$
∵$30-\frac{10}{3}=\frac{80}{3}＞25,$
∴经过适当的安排,能使学生在听这道题目的讲解时,专注度不低于60.(10分)