《2025年大联考单元期末测试卷九年级数学全一册沪科版》

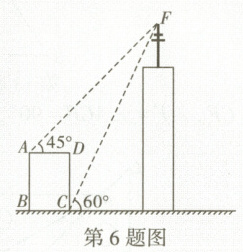
6. 【新情境】如图,某高楼顶部有一信号发射塔,在矩形建筑物 $ ABCD $ 的 $ A $, $ C $ 两点测得该塔顶端 $ F $ 的仰角分别为 $ 45° $ 和 $ 60° $,矩形建筑物的宽度 $ AD = 20 m $,高度 $ DC = 30 m $,则信号发射塔顶端 $ F $ 到地面的距离是 (C)

A.$ (35\sqrt{3} + 55) m $
B.$ (25\sqrt{3} + 45) m $
C.$ (25\sqrt{3} + 75) m $
D.$ (50 + 20\sqrt{2}) m $

答案： 6.C

7. 如图,在矩形 $ ABCD $ 中, $ AB = 3 $, $ AD = 5 $,点 $ E $ 在 $ DC $ 上,将矩形 $ ABCD $ 沿 $ AE $ 折叠,点 $ D $ 恰好落在边 $ BC $ 上的点 $ F $ 处,则 $ \cos \angle EFC $ 的值是 (C)

A.$ \frac{10}{3} $
B.$ \frac{2}{3} $
C.$ \frac{3}{5} $
D.$ \frac{5}{3} $

答案： 7.C

8. 如图,在等边三角形 $ ABC $ 中, $ AB = 2\sqrt{3} $,点 $ D $ 在边 $ AC $ 上, $ \tan \angle ABD = \frac{\sqrt{3}}{5} $,则 $ CD $ 的长为 (B)

A.$ \frac{5\sqrt{3}}{3} $
B.$ \frac{4\sqrt{3}}{3} $
C.2
D.$ \sqrt{3} $

答案： 8.B

9. 如图,在 $ Rt \triangle ABC $ 中, $ \angle C = 90° $, $ AC = 5\sqrt{3} $, $ AB = 10 $,则 $ \angle B = $60°.

答案： 9.60°

10. 如图,测量河宽 $ AB $ (假设河的两岸平行),在点 $ C $ 测得 $ \angle ACB = 30° $,在点 $ D $ 测得 $ \angle ADB = 60° $, $ CD = 60 m $,则河宽 $ AB $ 的长是30√3 $ m $ (结果保留根号).

答案： 10.30√3

11. 如图,在 $ Rt \triangle BAD $ 中,延长斜边 $ BD $ 至点 $ C $,使 $ DC = \frac{1}{2}BD $,连接 $ AC $. 若 $ \tan B = \frac{5}{3} $,则 $ \tan \angle CAD $ 的值是$\frac{1}{5}$.

答案： 11.$\frac{1}{5}$

12. 【核心素养·模型观念】如图 1 是某路灯,图 2 是此路灯在铅垂面内的示意图,灯芯 $ A $ 在地面上的照射区域 $ BC $ 长为 $ 7 m $,从 $ B $, $ C $ 两处测得灯芯 $ A $ 的仰角分别为 $ \alpha $ 和 $ \beta $,且 $ \tan \alpha = 6 $, $ \tan \beta = 1 $.
(1) 灯芯 $ A $ 到地面的高度为6 $ m $.
(2) 立柱 $ DE $ 的高为 $ 6 m $,灯杆 $ DF $ 与立柱 $ DE $ 的夹角 $ \angle D = 120° $,灯芯 $ A $ 到顶部 $ F $ 的距离为 $ 1 m $,且 $ DF \perp AF $,则灯杆 $ DF $ 的长度为√3 $ m $.

答案： 12.
(1)6
(2)√3