《2025年课堂点睛八年级数学上册人教版安徽专版》

11. 在$(x^{2}+8)(x^{2}-3x)$的展开式中,三次项的系数为 (C)
A.$8$
B.$-1$
C.$-3$
D.$-24$

答案： C

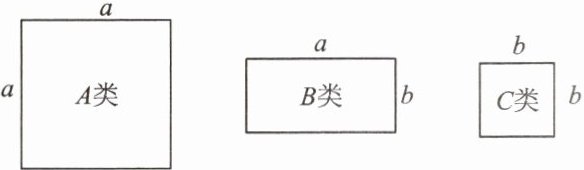
12. 【数形结合法】用如图所示的正方形和长方形卡片若干张拼成一个长为$2a + b$、宽为$a + 3b$的长方形,需要$A$类卡片2张,$B$类卡片7张,$C$类卡片3张.

答案： 2 7 3

13. 【新定义】$4个数a$,$b$,$c$,$d排列成\begin{vmatrix}a&b\\c&d\end{vmatrix} $,我们称之为二阶行列式,规定它的运算法则为$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc$.若$\begin{vmatrix}x - 2&x + 3\\x + 1&x - 2\end{vmatrix} = 13$,则$x$的值为$-\frac {3}{2}$.

答案： $-\frac {3}{2}$

14. 计算：
(1) $(a^{2}+3)(a - 2)-a(a^{2}-2a - 2)$；
(2) 已知$x^{2}-2x = 1$,求$(x - 1)(3x + 1)-(x + 1)^{2}$的值.

答案：
(1)解:原式$=a^{3}-2a^{2}+3a-6-a^{3}+2a^{2}+2a=5a-6$.
(2)解:原式$=3x^{2}+x-3x-1-x^{2}-2x-1=2x^{2}-4x-2,\because x^{2}-2x=1$,
∴原式$=2(x^{2}-2x)-2=2×1-2=0.$

15. 【代数推理】已知整式$A = 3m + 1$,$B = 3m - 1$,$m$为任意有理数.$A\cdot B + 1$的值可能为负数吗？请说明理由.

答案： 解:$A\cdot B+1$的值不可能为负数.理由:$\because A=3m+1,B=3m-1$,
∴$A\cdot B+1=(3m+1)(3m-1)+1=9m^{2}-3m+3m-1+1=9m^{2}≥0$,
∴$A\cdot B+1$的值不可能为负数.

16. 【数学与生活】如图①,在某住房小区的建设中,为了业主的宜居环境,小区准备在一个长为$(4a + 3b)$m,宽为$(2a + 3b)$m 的长方形草坪上修建一横一竖、宽度均为$b$m 的通道.
(1) 通道的面积为多少平方米？
(2) 若修建一横两竖、宽度均为$b$m 的通道(如图②),求剩余草坪的面积.

答案：
(1)解:$S_{通道}=b(2a+3b)+b(4a+3b)-b^{2}=2ab+3b^{2}+4ab+3b^{2}-b^{2}=(6ab+5b^{2})m^{2}$.故通道的面积为$(6ab+5b^{2})m^{2}$.
(2)$S_{草坪}=(2a+3b-b)(4a+3b-2b)=(2a+2b)(4a+b)=(8a^{2}+10ab+2b^{2})m^{2}$.故剩余草坪的面积为$(8a^{2}+10ab+2b^{2})m^{2}.$