第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
8. 如图,点$P是射线ON$上一动点(即$P可在射线ON$上运动),$\angle AON = 45^{\circ}$。当$\angle A = $
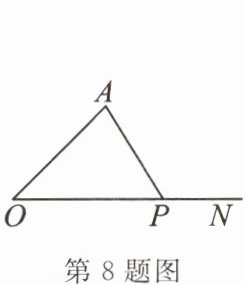
45°或67.5°或90°
时,$\triangle AOP$为等腰三角形。
答案:
45°或67.5°或90°
9. 如图,下列条件不能推出$\triangle ABC$是等腰三角形的是(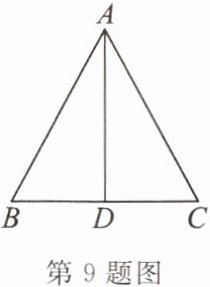
A.$\angle B = \angle C$
B.$AD \perp BC$,$\angle BAD = \angle CAD$
C.$AD \perp BC$,$\angle BAD = \angle ACD$
D.$AD \perp BC$,$BD = CD$
C
)
A.$\angle B = \angle C$
B.$AD \perp BC$,$\angle BAD = \angle CAD$
C.$AD \perp BC$,$\angle BAD = \angle ACD$
D.$AD \perp BC$,$BD = CD$
答案:
C
10. 将一张长方形纸片$ABCD$按图中那样折叠。若$AE = 3$,$AB = 4$,$BE = 5$,则重叠部分的面积为(
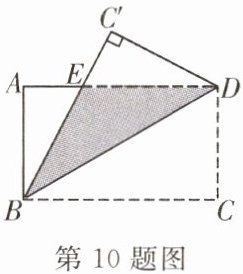
A.6
B.8
C.10
D.12
C
)
A.6
B.8
C.10
D.12
答案:
C
11. 【原创题】如图,一艘海轮位于灯塔$P的南偏东70^{\circ}方向的点M$处,它以$40海里/h$的速度向正北方向航行,$2h后到达位于灯塔P的北偏东40^{\circ}方向的点N$处,则点$N处与灯塔P$的距离为
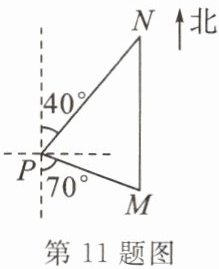
80
海里。
答案:
80
12. 在一次数学课上,王老师在屏幕上出示了一道例题:
如图,在$\triangle ABC$中,$D$,$E分别是AB$,$AC$边上的点,$BE与CD交于点O$,给出下列四个条件:①$\angle DBO = \angle ECO$;②$\angle BDO = \angle CEO$;③$BD = CE$;④$OB = OC$。
(1)要求同学从这四个条件中选出两个作为已知条件,用来判定$\triangle ABC$是等腰三角形。
请你在横线上用序号写出所有情形:
(2)选择(1)中的一种情形,写出证明过程。
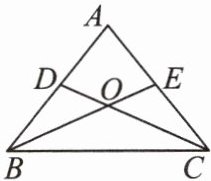
如图,在$\triangle ABC$中,$D$,$E分别是AB$,$AC$边上的点,$BE与CD交于点O$,给出下列四个条件:①$\angle DBO = \angle ECO$;②$\angle BDO = \angle CEO$;③$BD = CE$;④$OB = OC$。
(1)要求同学从这四个条件中选出两个作为已知条件,用来判定$\triangle ABC$是等腰三角形。
请你在横线上用序号写出所有情形:
①③,①④,②③,②④
;(2)选择(1)中的一种情形,写出证明过程。

答案:
(1)①③,①④,②③,②④(2)解:以①④为条件;
∵OB = OC,
∴∠OBC = ∠OCB.
∵∠DBO = ∠ECO,
∴∠DBO + ∠OBC = ∠ECO + ∠OCB,即∠DBC = ∠ECB,
∴AC = AB,即△ABC是等腰三角形.(答案不唯一)
∵OB = OC,
∴∠OBC = ∠OCB.
∵∠DBO = ∠ECO,
∴∠DBO + ∠OBC = ∠ECO + ∠OCB,即∠DBC = ∠ECB,
∴AC = AB,即△ABC是等腰三角形.(答案不唯一)
13. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,点$P是线段AC$上一点,过点$A作AB$的垂线,交$BP的延长线于点M$,$MN \perp AC于点N$,$PQ \perp AB于点Q$,$AQ = MN$。求证:
(1)$\triangle APM$是等腰三角形;
(2)$PC = AN$。
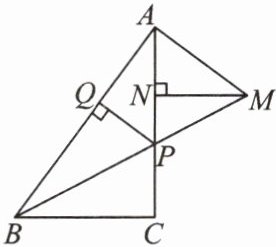
(1)$\triangle APM$是等腰三角形;
(2)$PC = AN$。

答案:
(1)证明:
∵BA⊥AM,MN⊥AC,
∴∠BAM = ∠ANM = 90°,
∴∠PAQ + ∠MAN = ∠MAN + ∠AMN = 90°,
∴∠PAQ = ∠AMN.
∵PQ⊥AB,MN⊥AC,
∴∠PQA = ∠ANM = 90°. 在△PQA和△ANM中,{∠PAQ = ∠AMN,AQ = MN,∠PQA = ∠ANM,}
∴△PQA≌△ANM(ASA),
∴AP = MA,
∴△APM是等腰三角形.(2)由(1)知△PQA≌△ANM,
∴PQ = AN,AP = MA,
∴∠AMB = ∠APM.
∵∠APM = ∠BPC,∠BPC + ∠PBC = 90°,∠AMB + ∠ABM = 90°,
∴∠ABM = ∠PBC.
∵PQ⊥AB,PC⊥BC,
∴PQ = PC,
∴PC = AN.
∵BA⊥AM,MN⊥AC,
∴∠BAM = ∠ANM = 90°,
∴∠PAQ + ∠MAN = ∠MAN + ∠AMN = 90°,
∴∠PAQ = ∠AMN.
∵PQ⊥AB,MN⊥AC,
∴∠PQA = ∠ANM = 90°. 在△PQA和△ANM中,{∠PAQ = ∠AMN,AQ = MN,∠PQA = ∠ANM,}
∴△PQA≌△ANM(ASA),
∴AP = MA,
∴△APM是等腰三角形.(2)由(1)知△PQA≌△ANM,
∴PQ = AN,AP = MA,
∴∠AMB = ∠APM.
∵∠APM = ∠BPC,∠BPC + ∠PBC = 90°,∠AMB + ∠ABM = 90°,
∴∠ABM = ∠PBC.
∵PQ⊥AB,PC⊥BC,
∴PQ = PC,
∴PC = AN.
查看更多完整答案,请扫码查看


