第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 如图,其中是全等三角形的是(
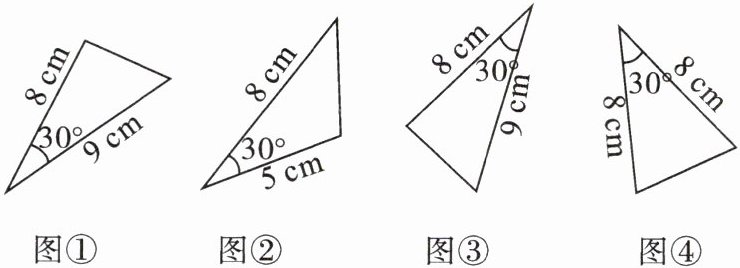
A.图①和图②
B.图②和图③
C.图②和图④
D.图①和图③
D
)
A.图①和图②
B.图②和图③
C.图②和图④
D.图①和图③
答案:
D
2. (湖南省中考改编)如图,$OA = OB$,要想用“SAS”证明$\triangle AOD\cong\triangle BOC$,还需添加一个条件:
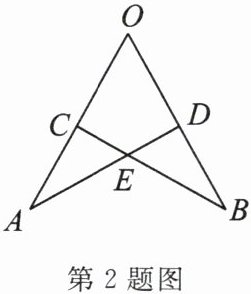
OC=OD(答案不唯一)
.
答案:
OC=OD(答案不唯一)
3. (湖北省中考改编)如图,在四边形 $ABCD$中,对角线 $AC$,$BD$ 相交于点 $O$,$OA = OC$,请你添加一个条件

OB=OD
,使$\triangle AOB\cong\triangle COD$.
答案:
OB=OD
4. (云南省中考)如图,在$\triangle ABC和\triangle AED$中,$AB = AE$,$\angle BAE= \angle CAD$,$AC = AD$.
求证:$\triangle ABC\cong\triangle AED$.
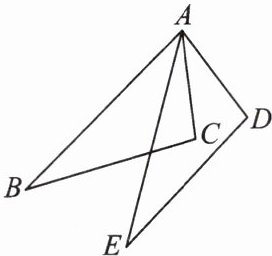
求证:$\triangle ABC\cong\triangle AED$.

答案:
证明:
∵∠BAE=∠CAD,
∴∠BAE+∠EAC=∠CAD+∠EAC,
∴∠BAC=∠EAD,在△ABC和△AED中,$\left\{\begin{array}{l} AB=AE,\\ ∠BAC=∠EAD,\\ AC=AD,\end{array}\right. $
∴△ABC≌△AED(SAS).
∵∠BAE=∠CAD,
∴∠BAE+∠EAC=∠CAD+∠EAC,
∴∠BAC=∠EAD,在△ABC和△AED中,$\left\{\begin{array}{l} AB=AE,\\ ∠BAC=∠EAD,\\ AC=AD,\end{array}\right. $
∴△ABC≌△AED(SAS).
5. (乐山市中考)如图,$AB是\angle CAD$的平分线,$AC = AD$,求证:$\angle C= \angle D$.
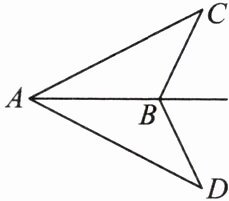

答案:
证明:
∵AB是∠CAD的平分线,
∴∠CAB=∠DAB,在△ABC和△ABD中,$\left\{\begin{array}{l} AC=AD,\\ ∠CAB=∠DAB,\\ AB=AB,\end{array}\right. $
∴△ABC≌△ABD(SAS),
∴∠C=∠D.
∵AB是∠CAD的平分线,
∴∠CAB=∠DAB,在△ABC和△ABD中,$\left\{\begin{array}{l} AC=AD,\\ ∠CAB=∠DAB,\\ AB=AB,\end{array}\right. $
∴△ABC≌△ABD(SAS),
∴∠C=∠D.
6. (教材第 34 页第 1 题变式)如图,$AA'$,$BB'$表示两根长度相同的木条,若点 $O$ 是 $AA'$,$BB'$的中点,经测量 $AB = 6cm$,则容器的内径 $A'B'$的长为(

A.$5cm$
B.$6cm$
C.$7cm$
D.$8cm$
B
)
A.$5cm$
B.$6cm$
C.$7cm$
D.$8cm$
答案:
B
7. 【新考法】如图所示,有一块三角形镜子,小明不小心将它打破成①,②两块,现需配成同样大小的一块. 为了方便起见,需带上

①
,理由是“SAS
”. (用字母表示)
答案:
① SAS
8. 如图,$AC = AD$,$AE = AB$,要使$\triangle ABC\cong\triangle AED$,应添加的条件是(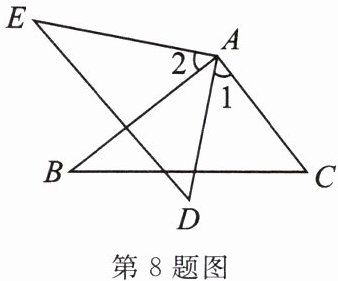
A.$\angle 1= \angle 2$
B.$\angle B= \angle E$
C.$\angle C= \angle D$
D.$\angle B= \angle C$
A
)
A.$\angle 1= \angle 2$
B.$\angle B= \angle E$
C.$\angle C= \angle D$
D.$\angle B= \angle C$
答案:
A
查看更多完整答案,请扫码查看


