第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
9. 如图,在 $\triangle ABC$ 中,分别以点 $B$ 和点 $C$ 为圆心,大于 $\frac{1}{2}BC$ 长为半径画弧,两弧相交于点 $M$,$N$,作直线 $MN$,交 $AC$ 于点 $D$,交 $BC$ 于点 $E$,连接 $BD$. 若 $AB = 7$,$AC = 12$,$BC = 6$,则 $\triangle ABD$ 的周长为(
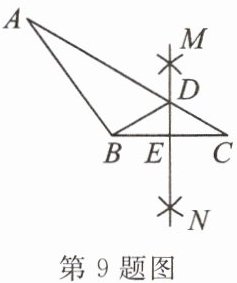
A.25
B.22
C.19
D.18
C
)
A.25
B.22
C.19
D.18
答案:
C
10. 【原创题】如图,已知直线 $l$ 及直线 $l$ 外一点 $P$,观察图中的尺规作图痕迹,则下列结论不一定成立的是______(填序号).
① $PQ$ 为直线 $l$ 的垂线;② $CA = CB$;③ $PO = QO$;④ $\angle APO = \angle BPO$.
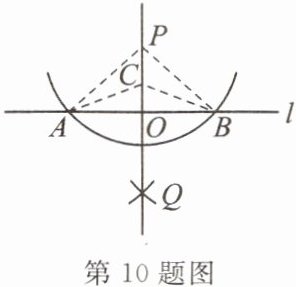
① $PQ$ 为直线 $l$ 的垂线;② $CA = CB$;③ $PO = QO$;④ $\angle APO = \angle BPO$.

③
答案:
③
11. 如图,校园内有两条路 $OA$,$OB$,在交叉口附近有两块宣传牌 $C$,$D$,学校准备安装一盏路灯,要求灯柱 $P$ 的位置到两块宣传牌的距离相等,并且到两条路的距离也相等,请你帮忙画出灯柱 $P$ 的位置.
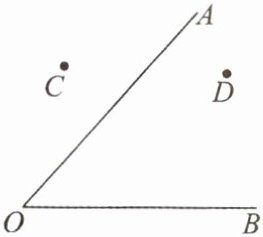

答案:
解:如图,点P即为所求.
解:如图,点P即为所求.

12. 如图,$\triangle ABC$ 和 $\triangle A'B'C'$ 关于直线 $MN$ 对称,$\triangle A'B'C'$ 和 $\triangle A''B''C''$ 关于直线 $EF$ 对称.
(1)画出直线 $EF$;
(2)直线 $MN$ 与 $EF$ 相交于点 $O$,试探究 $\angle BOB''$ 与直线 $MN$,$EF$ 所夹锐角 $\alpha$ 的数量关系.
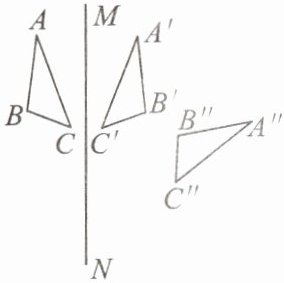
(1)画出直线 $EF$;
(2)直线 $MN$ 与 $EF$ 相交于点 $O$,试探究 $\angle BOB''$ 与直线 $MN$,$EF$ 所夹锐角 $\alpha$ 的数量关系.

答案:
(1)解:如图所示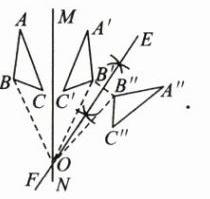
(2)连接BO、B'O、B''O,
∵△ABC 和△A'B'C'关于直线MN对称,
∴∠BOM=∠B'OM. 又
∵△A'B'C'和△A''B''C''关于直线EF对称,
∴∠B'OE=∠B''OE.
∴∠BOB''=∠BOM+∠B'OM+∠B'OE+∠B''OE=2(∠B'OM+∠B'OE)=2α,即∠BOB''=2α.
(1)解:如图所示

(2)连接BO、B'O、B''O,
∵△ABC 和△A'B'C'关于直线MN对称,
∴∠BOM=∠B'OM. 又
∵△A'B'C'和△A''B''C''关于直线EF对称,
∴∠B'OE=∠B''OE.
∴∠BOB''=∠BOM+∠B'OM+∠B'OE+∠B''OE=2(∠B'OM+∠B'OE)=2α,即∠BOB''=2α.
13. 【核心素养·模型观念】
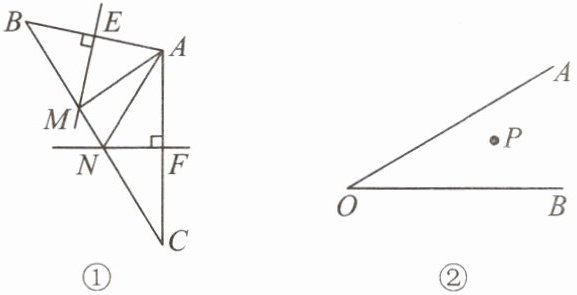
(1)如图①,在 $\triangle ABC$ 中,直线 $ME$ 垂直平分 $AB$,分别交 $AB$,$BC$ 于点 $E$,$M$,直线 $NF$ 垂直平分 $AC$,分别交 $AC$,$BC$ 于点 $F$,$N$. 求证:$\triangle AMN$ 的周长等于 $BC$ 的长;
(2)如图②,在 $\angle AOB$ 的内部有一定点 $P$,试分别在 $OA$,$OB$ 上确定 $C$,$D$ 两点,使得 $\triangle PCD$ 的周长最短(保留作图痕迹,不写作法).
(1)如图①,在 $\triangle ABC$ 中,直线 $ME$ 垂直平分 $AB$,分别交 $AB$,$BC$ 于点 $E$,$M$,直线 $NF$ 垂直平分 $AC$,分别交 $AC$,$BC$ 于点 $F$,$N$. 求证:$\triangle AMN$ 的周长等于 $BC$ 的长;
(2)如图②,在 $\angle AOB$ 的内部有一定点 $P$,试分别在 $OA$,$OB$ 上确定 $C$,$D$ 两点,使得 $\triangle PCD$ 的周长最短(保留作图痕迹,不写作法).

答案:
(1)证明:
∵直线ME垂直平分AB,
∴BM=AM.
∵直线NF垂直平分AC,
∴AN=CN.将△AMN 的周长记为$C_{\triangle AMN}$.
∴$C_{\triangle AMN}=AM +MN+AN=BM+MN+CN=BC$,即△AMN的周长等于BC的长.
(2)解:如图②△PCD即为所求.
(1)证明:
∵直线ME垂直平分AB,
∴BM=AM.
∵直线NF垂直平分AC,
∴AN=CN.将△AMN 的周长记为$C_{\triangle AMN}$.
∴$C_{\triangle AMN}=AM +MN+AN=BM+MN+CN=BC$,即△AMN的周长等于BC的长.
(2)解:如图②△PCD即为所求.
查看更多完整答案,请扫码查看


