《2025年课堂点睛八年级数学上册人教版安徽专版》

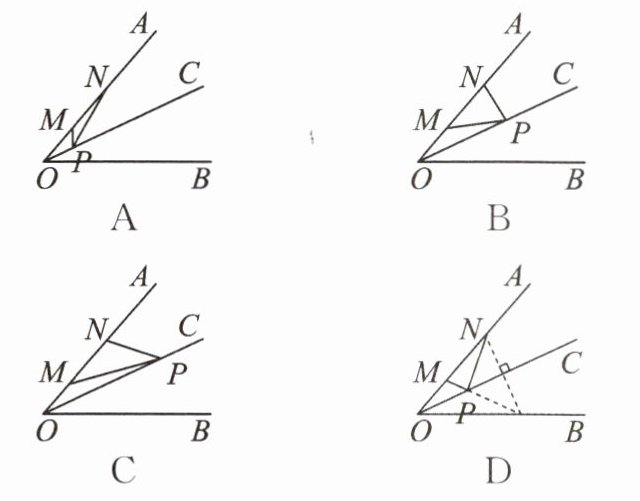
9. $ \angle AOB $ 的边 $ OA $ 上有 $ M $,$ N $ 两点,在 $ \angle AOB $ 的平分线 $ OC $ 上找一点 $ P $,使 $ MP + NP $ 最小,正确的作法是(D)

答案： D

10. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ BC = 4 $,$ \triangle ABC $ 的面积是 $ 14 $,$ AC $ 的垂直平分线 $ EF $ 分别交 $ AC $,$ AB $ 于 $ E $,$ F $ 点。若点 $ D $ 为 $ BC $ 边的中点,点 $ M $ 为线段 $ EF $ 上一动点,则 $ CM + DM $ 的最小值为(B)

A.$ 21 $
B.$ 7 $
C.$ 4 $
D.$ 2 $

答案： B

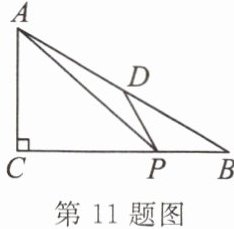
11. (随州市期末)如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \angle B = 30^{\circ} $,$ BC = 8 $,$ D $ 为 $ AB $ 的中点,$ P $ 为 $ BC $ 上一动点,连接 $ AP $,$ DP $,则 $ AP + DP $ 的最小值是8。

答案： 8

12. 【原创题】如图,$ OE $ 为 $ \angle AOB $ 的平分线,$ \angle AOB = 30^{\circ} $,$ OB = 6 $,点 $ P $,$ C $ 分别为射线 $ OE $,$ OB $ 上的动点,求 $ PC + PB $ 的最小值。

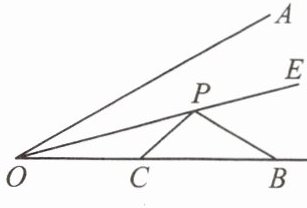
答案： 解:在OA上截取OD=OC,连接PD,易证△POC≌△POD(SAS),
∴PD=PC,过点B作BF⊥OA于点F,
∵∠AOB=30°,
∴BF= $\frac{1}{2}$OB=3,
∴PC+PB=PD+PB≥BF=3,故PC+PB的最小值为3.

13. 【项目式学习】如图①,$ A $,$ B $ 两地在一条河的两岸,现要在河上造一座桥 $ MN $,桥造在何处才能使从 $ A $ 到 $ B $ 的路径 $ AMNB $ 最短？(假定河的两岸是平行的直线,桥要与河垂直)
【思考】如图②,如果 $ A $,$ B $ 两地之间有两条平行的河流,我们要建的桥都是要与河岸垂直的,我们应该如何找到这个最短的距离？
【进一步思考】如图③,如果 $ A $,$ B $ 两地之间有三条平行的河流,该如何确定桥的位置？
【拓展】如图④,如果在上述其他条件不变的情况下,两条河并不平行,又该如何确定桥的位置？
请将你的思考在下面准备好的图形中表示出来,保留作图痕迹,将行走的路线用实线画出来。

答案：
解:如图①所示，从A到B的路径AMNB最短.　　 [思考]如图②所示,从A到B的路径AMNEFB最短.[进一步思考]如图③所示，从A到B的路径AMNGHFEB最短.[拓展]如图④所示，从A到B的路径AMNEFB最短.