《2025年配套综合练习甘肃九年级数学上册人教版》

15. 如图 24 - 2 - 4,$ A $,$ B $,$ C $ 为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,要使回收站建在距离三个小区都相等的某处. 请问：如果你是工程师,你将如何选址？

答案：
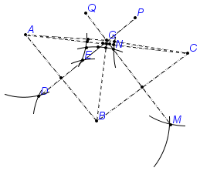
提示：找以A,B,C为顶点的三角形的外心，作△ABC中任意两条边的垂直平分线，交点即为所求.

16. (选做题)在 $ \triangle ABC $ 中,$ AB = 1 $,$ AC $,$ BC $ 是关于 $ x $ 的一元二次方程 $ (m + 5)x^{2} - (2m - 5)x + 12 = 0 $ 的两个根,$ \triangle ABC $ 的外接圆 $ \odot O $ 的面积为 $ \dfrac{\pi}{4} $,求 $ m $ 的值.

答案： 解：设⊙O的半径为r，由$πr^{2}=\frac{π}{4}$，得$r=\frac{1}{2}$.由AB=1知AB是直径，所以△ABC是直角三角形，∠ACB=90°.所以$AC^{2}+BC^{2}=1$.由一元二次方程根与系数的关系，得AC+BC=$\frac{2m-5}{m+5}$，AC·BC=$\frac{12}{m+5}$.由$AC^{2}+BC^{2}=(AC+BC)^{2}-2AC·BC=1$，解得$m_{1}=20$，$m_{2}=-2$.因为关于x的一元二次方程$(m+5)x^{2}-(2m-5)·x+12=0$有两个根，所以m要满足Δ≥0且m+5≠0.当m=20时，满足；当m=-2时，Δ＜0（舍去）.所以m=20.

17. 画边长为 $ 3\ cm $ 的正方形 $ ABCD $(如图 22 - 2 - 5),连接 $ AC $,$ BD $ 相交于点 $ O $,以点 $ A $ 为圆心,$ 2\sqrt{2}\ cm $ 长为半径画圆,试判断点 $ B $,$ C $,$ D $,$ O $ 四点与这个圆的位置关系.

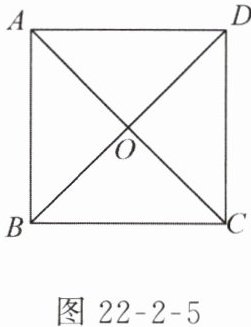
答案： 解：因为AB=BC=3，∠ABC=90°，所以用勾股定理得到$AC=3\sqrt{2}$.又因为正方形的对角线互相平分，所以$AO=\frac{3\sqrt{2}}{2}$.因为$AB=3＞2\sqrt{2}$，所以点 B 在圆外.因为$AC=3\sqrt{2}＞2\sqrt{2}$，所以点 C 在圆外.因为$AD=3＞2\sqrt{2}$，所以点 D 在圆外.因为$AO=\frac{3\sqrt{2}}{2}＜2\sqrt{2}$，所以点 O 在圆内.