《2025年配套综合练习甘肃九年级数学上册人教版》

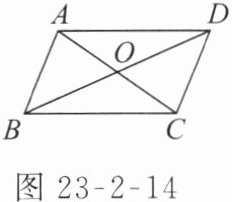
11. 如图 23 - 2 - 14,$ □ ABCD $ 是中心对称图形,点O是旋转中心,旋转了180度后能与自身重合,则 $ AD = $BC,$ AO = $CO,$ BO = $DO.

答案： O 180 BC CO DO

12. 若 $ O $ 是 $ □ ABCD $ 的对角线 $ AC $ 的中点,$ EF \perp AC $ 于点 $ O $,分别交 $ AD $,$ BC $ 于点 $ E $,$ F $,那么线段 $ DE $ 关于点 $ O $ 的对称线段为BF.

答案： BF

13. 写出一个图象关于原点成中心对称,且经过第二、四象限的函数表达式：y=-x(答案不唯一).

答案： y=-x(答案不唯一)

14. 观察图 23 - 2 - 15,将其中轴对称图形、旋转对称图形和中心对称图形所对应的序号分别填入相应的圈内.

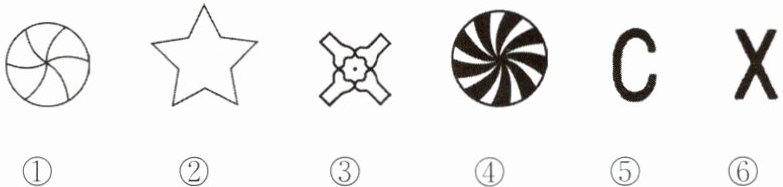
答案： ②③⑤⑥ ①②③④⑥ ①③⑥

15. 如图 23 - 2 - 16,将 $ \triangle BOD $ 绕点 $ O $ 旋转 $ 180^{\circ} $ 后得到 $ \triangle AOC $,再过点 $ O $ 任意画一条与 $ AC $,$ BD $ 都相交的直线 $ MN $,交点分别为 $ M $ 和 $ N $,试问：线段 $ OM = ON $ 成立吗？若成立,请进行证明；若不成立,请说明理由.

答案： OM=ON 成立.提示:通过证△AOM≌△BON达到目的.