《2025年配套综合练习甘肃九年级数学上册人教版》

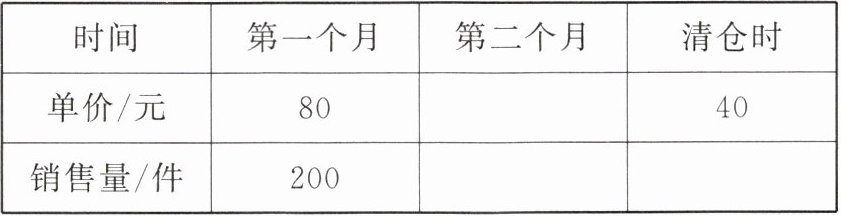
15. 某批发商以每件 50 元的价格购进 800 件 T 恤. 第一个月以单价 80 元销售,售出了 200 件；第二个月如果单价不变,预计仍可售出 200 件,批发商为增加销售量,决定降价销售. 根据市场调查,单价每降低 1 元,可多售出 10 件,但最低单价应高于购进的价格；第二个月结束后,批发商将对剩余的 T 恤一次性清仓销售,清仓时单价为 40 元. 设第二个月的单价降低 $ x $ 元.
(1)填表 21 - 3 - 1(不需要化简)：

(2)如果批发商希望通过销售这批 T 恤获利 9000 元,那么第二个月的单价应是多少元?

答案：
(1)80-x 200+10x 800-200-(200+10x)
(2)根据题意,得80×200+(80-x)(200+10x)+40[800-200-(200+10x)]-50×800=9000.整理,得x²-20x+100=0.解这个方程,得x₁=x₂=10.当x=10时,80-x=70＞50.答:第二个月的单价应是70元.

16. (选做题)将一根长为 20 cm 的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于 $ 17 cm^{2} $,那么这根铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于 $ 12 cm^{2} $ 吗? 若能,求出两段铁丝的长度；若不能,请说明理由.

答案：
(1)设其中一个正方形的边长为x cm,则另一个正方形的边长为$\frac{20-4x}{4}=5-x$(cm).依题意列方程,得x²+(5-x)²=17.解方程,得x₁=1,x₂=4.因此,这根铁丝剪成两段后的长度分别是4 cm,16 cm.
(2)两个正方形的面积之和不可能等于12cm².理由:因为两个正方形的面积和为x²+(5-x)²=$2(x-\frac{5}{2})^2+\frac{25}{2}$≥12.5＞12,所以两个正方形的面积之和不可能等于12cm².