《2025年配套综合练习甘肃九年级数学上册人教版》

9. 当炮弹从炮口以 $ 30^{\circ} $ 角射出后,飞行高度 $ h $(m)与飞行时间 $ t $(s)之间的函数关系是 $ h = \frac{1}{2}v_{0}t - 5t^{2} $,其中 $ v_{0} $ 是炮弹发射的初速度. 当 $ v_{0} = 300 $ m/s 时,炮弹飞行的最大高度是1125m.

答案： 1125

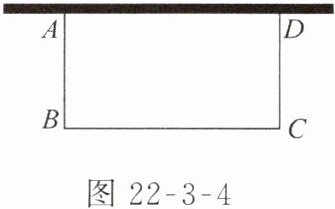
10. 如图 22-3-4,王叔叔想用长为 60 m 的栅栏,再借助房屋的外墙围成一个矩形羊圈 $ ABCD $,已知房屋外墙足够长,当矩形 $ ABCD $ 的边 $ AB = $15m 时,羊圈的面积最大.

答案： 15

11. 人民币一年定期的年利率为 $ x $,一年到期后,银行将本金和利息自动按一年定期储蓄转存. 若存款额是 $ a $ 元,则两年后的本息和 $ y $(元)关于 $ x $ 的表达式为$y=a(1+x)^2$.

答案： $y=a(1+x)^2$

12. 如图 22-3-5,某大桥有一段抛物线形的拱梁,抛物线的表达式为 $ y = ax^{2}+bx $. 小强骑自行车从拱梁一端 $ O $ 沿直线匀速穿过拱梁部分的桥面 $ OC $,当小强骑自行车行驶 10 s 和 26 s 时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面 $ OC $ 共需36s.

答案： 36

13. 某商场销售一批名牌衬衫,平均每天可售出 20 件,每件赢利 40 元. 为了提高销售量,增加利润,尽快减少库存,该商场决定采取适当的降价措施. 经调查,发现：如果每件衬衫每降价 1 元,该商场平均每天可多售出 2 件. 该商场降价后每天赢利 $ y $(元)与降价 $ x $(元)之间的函数关系为$y=-2x^2+60x+800$. (不考虑 $ x $ 的取值范围)

答案： $y=-2x^2+60x+800$

14. 如图 22-3-6①,三孔桥截面的三个孔都呈抛物线形,两个小孔形状、大小都相同. 如图 22-3-6②,正常水位时,大孔水面宽度 $ AB = 20 $ m,顶点 $ M $ 距水面 6 m(即 $ MO = 6 $ m),小孔顶点 $ N $ 距水面 4.5 m(即 $ NC = 4.5 $ m). 当水位上涨刚好淹没小孔时,求此时大孔的水面宽度 $ EF $.

答案： 解:设大孔所在抛物线的表达式为$y=ax^2+6$,把点$A(-10,0)$的坐标代入表达式,得$a=-\dfrac{3}{50}$.所以大孔所在抛物线的表达式为$y=-\dfrac{3}{50}x^2+6$.由$NC=4.5\ m$可知,点$F$的纵坐标为4.5,代入表达式$y=-\dfrac{3}{50}x^2+6$,解得$x=\pm5$.由抛物线的对称性可知,点$E(-5,4.5)$,点$F(5,4.5)$,所以$EF=10\ m$.