第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
2. 某商店经营皮鞋,已知所获利润 $ y $(元)与销售单价 $ x $(元)之间的关系为 $ y = -x^{2}+24x + 2956 $,则获利最多为(
A.3144 元
B.3100 元
C.144 元
D.2956 元
B
).A.3144 元
B.3100 元
C.144 元
D.2956 元
答案:
B
3. 某大学的校门是一抛物线形水泥建筑物(如图 22-3-8),大门的地面宽度为 8 m,两侧距地面 4 m 高处各有一个挂校名匾用的铁环,两铁环的水平距离为 6 m,则校门的高度约为(结果精确到 0.1 m,水泥建筑物的厚度忽略不计)(

A.5.1 m
B.9 m
C.9.1 m
D.9.3 m
C
).
A.5.1 m
B.9 m
C.9.1 m
D.9.3 m
答案:
C
4. 已知某幢建筑物,从 10 m 高的窗口 $ A $ 处用水管向外喷水,喷出的水流呈抛物线状(抛物线所在平面与墙面垂直,如图 22-3-9). 若抛物线的最高点 $ P $ 离墙 1 m,离地面 $ \frac{40}{3} $ m,则水流落地点 $ B $ 离墙的距离 $ OB $ 是(
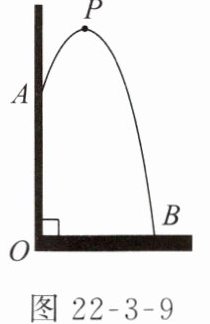
A.2 m
B.3 m
C.4 m
D.5 m
B
).
A.2 m
B.3 m
C.4 m
D.5 m
答案:
B
5. 二次函数 $ y = 2x^{2}-8x + 9 $ 的图象的对称轴是直线
x=2
,顶点坐标是 (2,1)
. 当 $ x = $2
时,函数有最 小
值,是 1
.
答案:
x=2 (2,1) 2 小 1
6. 图 22-3-10 是一学生推铅球时,铅球行进的高度 $ y $(m) 与水平距离 $ x $(m) 的函数图象. 铅球推出的距离是

4+4√3
m.
答案:
4+4√3
7. 用长度一定的绳子围成一个矩形,如果矩形的一边长 $ x $(m)与面积 $ y $(m^2)满足函数关系式 $ y = -(x - 12)^{2}+144(0 < x < 24) $,那么该矩形面积的最大值是
144
m^2.
答案:
144
8. 某隧道的截面是抛物线,且抛物线的表达式为 $ y = -\frac{1}{8}x^{2}+3.25 $,一辆车高 3 m,宽 4 m,该车
不能
通过该隧道. (选填“能”或“不能”)
答案:
不能
查看更多完整答案,请扫码查看


