《2025年配套综合练习甘肃九年级数学上册人教版》

5. 给出下列现象:①地下水位逐年下降;②传送带上物体的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千. 其中属于旋转的有③④⑤⑥. (填序号)

答案： ③④⑤⑥

6. 等边三角形绕其中心至少旋转120度才能与自身重合.

答案： 120

7. 正方形绕其中心旋转一定的角度与原图形重合,则这个旋转角度至少为90度.

答案： 90

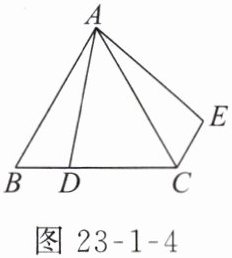
8. 如图 23 - 1 - 4,在等边三角形 $ABC$ 中,$AB = 6$,$D$ 是 $BC$ 上一点,且 $BC = 3BD$,$\triangle ABD$ 绕点 $A$ 旋转后得到 $\triangle ACE$,则 $CE$ 的长度为2.

答案： 2

9. 如图 23 - 1 - 5,$O$ 是等边三角形 $ABC$ 内一点,将 $\triangle AOB$ 绕 $A$ 点逆时针旋转,使 $B$,$O$ 两点的对应点分别为 $C$,$D$,则旋转角的度数为60°;图中除 $\triangle ABC$ 外,还是等边三角形的是△AOD.

答案： 60° △AOD

10. 如图 23 - 1 - 6,六角星可看作是由什么“基本图形”通过怎样的旋转而得到的?

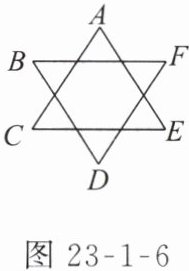
答案： 基本图形是六角星的六分之一部分（如由中心与相邻两个顶点构成的三角形），绕六角星的中心按顺时针（或逆时针）方向旋转60°，连续旋转5次得到整个六角星。