《2025年配套综合练习甘肃九年级数学上册人教版》

17. (选做题)一辆电动车在行驶过程中,前 $ 10s $ 行驶的路程 $ s(m) $ 与时间 $ t(s) $ 满足关系式 $ s = at^{2} $,第 $ 10s $ 末开始匀速行驶,第 $ 24s $ 末开始刹车,第 $ 28s $ 末停止行驶,此时离终点 $ 20m $ 远,图 22 - 1 - 3 是电动车行驶过程记录的图象。
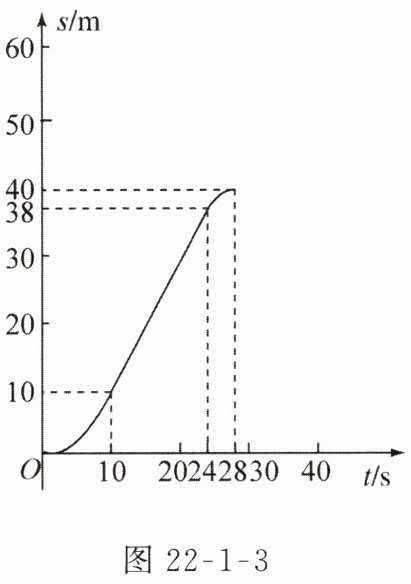
(1) 求电动车从出发到开始刹车时的路程 $ s(m) $ 与时间 $ t(s) $ 的函数关系式。
(2) 如果第 $ 24s $ 末不刹车继续匀速行驶,那么出发多少秒后通过终点？
(3) 如果 $ 10s $ 后仍按 $ s = at^{2} $ 的运动方式行驶,那么出发多长时间后通过终点(参考数据：$ \sqrt{6} \approx 2.45 $,计算结果精确到整数)？

答案： 解:
(1)当$0\leqslant t\leqslant10$时,点$(10,10)$在函数$s=at^{2}$的图象上,解得$a=\frac{1}{10}$,$s=\frac{1}{10}t^{2}$.当$10\leqslant t\leqslant24$时,函数关系式可设为一次函数$s=kt+b(k\neq0)$.因为函数图象过$(10,10)$,$(24,38)$两点,配套综合练习 数学 九年级上册所以$\begin{cases}10=10k+b,\\38=24k+b.\end{cases}$解得$\begin{cases}k=2,\\b=-10.\end{cases}$故$s=2t-10$.所以当$0\leqslant t\leqslant10$时,$s=\frac{t^{2}}{10}$;当$10\leqslant t\leqslant24$时,$s=2t-10$.
(2)当$s=40+20=60$时,$60=2t-10$,$t=35$,即如果第24s末不刹车继续匀速行驶,那么出发35s后通过终点.
(3)当$s=60$时,由$s=\frac{1}{10}t^{2}$,可得$60=\frac{1}{10}t^{2}$,$t=\pm\sqrt{600}=\pm10\sqrt{6}$(舍去负值).所以$t\approx25$,即出发约25s后通过终点.

1. 下列二次函数的图象开口一定向上的是(C)。
A.$ y = - 3 x ^ { 2 } + 1 $
B.$ y = a x ^ { 2 } - 3 $
C.$ y = \frac { 1 } { 3 } x ^ { 2 } - 2 $
D.$ y = ( a - 1 ) x ^ { 2 } - 5 $

答案： C

2. 将二次函数 $ y = - 2 x ^ { 2 } $ 的图象向下平移 $ 5 $ 个单位长度,得到的抛物线的表达式是(B)。
A.$ y = 2 x ^ { 2 } + 5 $
B.$ y = - 2 x ^ { 2 } - 5 $
C.$ y = - 2 x ^ { 2 } + 5 $
D.$ y = 2 x ^ { 2 } - 5 $

答案： B