《2025年同步练习册山东科学技术出版社八年级数学上册鲁教版五四制》

11. 给出下列多项式：① $ x^{2}+y^{2} $；② $ - x^{2}+y^{2} $；③ $ x^{2}+2 x y + y^{2} $；④ $ x^{4}-1 $；⑤ $ x(x + 1)-2(x + 1) $；⑥ $ m^{2}-m n+\frac{1}{4} n^{2} $。其中,能因式分解的是②③④⑤⑥。(填序号)

答案： ②③④⑤⑥

12. 已知 $ a + b = 3 $,$ a b = 2 $,则代数式 $ a^{3} b + 2 a^{2} b^{2}+a b^{3} $ 的值为18。

答案： 18

13. 给出下面一列单项式：$ - x $,$ \frac{1}{2} x^{2} $,$ -\frac{1}{4} x^{3} $,$ \frac{1}{8} x^{4} $,$ -\frac{1}{16} x^{5} $,…,其中 $ x eq 0 $。按此规律,第 11 个单项式是$-\dfrac{x^{11}}{2^{10}}$。

答案： $-\dfrac{x^{11}}{2^{10}}$

14. 若关于 $ x $ 的分式方程 $ \frac{x + k}{x + 1}+\frac{2 x}{x + 1}= 1 $ 的解为非正数,则 $ k $ 的取值范围是$k\geqslant1$,且$k\neq3$。

答案： $k\geqslant1$,且$k\neq3$

15. 已知 10 个数的平均数是 3,极差是 4,则将这 10 个数都扩大 10 倍,这组数据的平均数是30,极差是40。

答案： 30 40

16. 已知一组数据 $ x_{1} $,$ x_{2} $,$ x_{3} $,$ x_{4} $,$ x_{5} $ 的平均数是 2,那么另一组数据 $ 3 x_{1}-2 $,$ 3 x_{2}-2 $,$ 3 x_{3}-2 $,$ 3 x_{4}-2 $,$ 3 x_{5}-2 $ 的平均数是4。

答案： 4

三、解答题(共 56 分)
17. (8 分)先仔细阅读下面的例题,再解答问题。
例题：已知多项式 $ x^{2}-4 x + m $ 有一个因式是 $ x + 3 $,求另一个因式及 $ m $ 的值。
解：设另一个因式为 $ x + n $,
则 $ x^{2}-4 x + m= (x + 3)(x + n) $。
$ \therefore x^{2}-4 x + m= x^{2}+(n + 3) x + 3 n $。
$ \therefore\left\{\begin{array}{l}n + 3 = - 4,\\ m = 3 n.\end{array} \right. $
解得 $ n = - 7 $,$ m = - 21 $。
$ \therefore $ 另一个因式为 $ x - 7 $,$ m $ 的值为 - 21。
问题：已知多项式 $ 2 x^{2}+3 x - k $ 有一个因式是 $ 2 x - 5 $,求另一个因式及 $ k $ 的值。

答案： 17. 解:设另一个因式为$x+a$,则$2x^{2}+3x-k=(2x-5)(x+a)$.$\therefore 2x^{2}+3x-k=2x^{2}+(2a-5)x-5a$.$\therefore \begin{cases} 2a-5=3, \\ -5a=-k. \end{cases}$解得$a=4$,$k=20$.故另一个因式为$x+4$,$k$的值为20.
18.
(1)$m^{2}-3m=m(m-3)$.
(2)原式$=(a-b)^{2}-2(a-b)=(a-b)(a-b-2)$.
(3)$(4x-y)^{2}+y(y-4x)^{2}=(4x-y)^{2}(1+y)$.

18. (9 分)因式分解：
(1)$ m^{2}-3 m $；
(2)$ (a - b)^{2}-2 a + 2 b $；
(3)$ (4 x - y)^{2}+y(y - 4 x)^{2} $。

答案： 1. （1）
解：对于$m^{2}-3m$，提取公因式$m$，可得$m(m - 3)$。
2. （2）
解：
先对$(a - b)^{2}-2a + 2b$变形，$(a - b)^{2}-2a + 2b=(a - b)^{2}-2(a - b)$。
然后提取公因式$(a - b)$，得到$(a - b)(a - b - 2)$。
3. （3）
解：
对$(4x - y)^{2}+y(y - 4x)^{2}$变形，$(4x - y)^{2}+y(y - 4x)^{2}=(4x - y)^{2}+y(4x - y)^{2}$。
提取公因式$(4x - y)^{2}$，则$(4x - y)^{2}(1 + y)$。
综上，（1）$m(m - 3)$；（2）$(a - b)(a - b - 2)$；（3）$(4x - y)^{2}(1 + y)$。

19. (8 分)数学课上,李老师在黑板上写出下面一列有规律的分式：$ \frac{x^{3}}{y} $,$ -\frac{x^{5}}{y^{2}} $,$ \frac{x^{7}}{y^{3}} $,$ -\frac{x^{9}}{y^{4}} $,…,其中 $ x y eq 0 $。
(1)任意一个分式除以前面一个分式,你发现了什么规律？
(2)根据你发现的规律,试写出给定的这列分式中的第 7 个分式。

答案： 1. （1）
解：设这列分式为$a_{n}$，$a_{1}=\frac{x^{3}}{y}$，$a_{2}=-\frac{x^{5}}{y^{2}}$，$a_{3}=\frac{x^{7}}{y^{3}}$，$a_{4}=-\frac{x^{9}}{y^{4}}$。
计算$\frac{a_{2}}{a_{1}}$：
$\frac{a_{2}}{a_{1}}=\frac{-\frac{x^{5}}{y^{2}}}{\frac{x^{3}}{y}}=-\frac{x^{5}}{y^{2}}\cdot\frac{y}{x^{3}}=-\frac{x^{5 - 3}}{y^{2 - 1}}=-\frac{x^{2}}{y}$。
计算$\frac{a_{3}}{a_{2}}$：
$\frac{a_{3}}{a_{2}}=\frac{\frac{x^{7}}{y^{3}}}{-\frac{x^{5}}{y^{2}}}=\frac{x^{7}}{y^{3}}\cdot(-\frac{y^{2}}{x^{5}})=-\frac{x^{7 - 5}}{y^{3 - 2}}=-\frac{x^{2}}{y}$。
计算$\frac{a_{4}}{a_{3}}$：
$\frac{a_{4}}{a_{3}}=\frac{-\frac{x^{9}}{y^{4}}}{\frac{x^{7}}{y^{3}}}=-\frac{x^{9}}{y^{4}}\cdot\frac{y^{3}}{x^{7}}=-\frac{x^{9 - 7}}{y^{4 - 3}}=-\frac{x^{2}}{y}$。
规律：任意一个分式除以前面一个分式的结果都为$-\frac{x^{2}}{y}$。
2. （2）
解：由（1）可知这列分式的规律：
第$n$个分式$a_{n}=(-1)^{n + 1}\frac{x^{2n+1}}{y^{n}}$（$n$为正整数）。
当$n = 7$时：
$a_{7}=(-1)^{7 + 1}\frac{x^{2×7 + 1}}{y^{7}}$。
根据$(-1)^{8}=1$，$2×7+1 = 15$，所以$a_{7}=\frac{x^{15}}{y^{7}}$。
综上，（1）规律是任意一个分式除以前面一个分式的结果都为$-\frac{x^{2}}{y}$；（2）第$7$个分式为$\frac{x^{15}}{y^{7}}$。

20. (9 分)阅读下列材料：
对于两个不相等的非零实数 $ a $,$ b $,若分式 $ \frac{(x - a)(x - b)}{x} $ 的值为 0,则 $ x = a $ 或 $ x = b $。
又因为 $ \frac{(x - a)(x - b)}{x}= \frac{x^{2}-(a + b) x + a b}{x}= x+\frac{a b}{x}-(a + b) $,所以关于 $ x $ 的方程 $ x+\frac{a b}{x}= a + b $ 有两个解,分别为 $ x_{1}= a $,$ x_{2}= b $。
应用上面的结论解答下列问题：
(1)求方程 $ x+\frac{8}{x}= 6 $ 的两个解中较大的一个；
(2)设关于 $ x $ 的方程 $ x+\frac{m - n}{m n x}= \frac{m + 4 m n - n}{2 m n} $ 的两个解分别为 $ x_{1} $,$ x_{2} $($ x_{1} \lt x_{2} $),若 $ x_{1} $ 与 $ x_{2} $ 互为倒数,求 $ x_{1} $,$ x_{2} $；
(3)设关于 $ x $ 的方程 $ 2 x+\frac{n^{2}+2 n - 3}{2 x - 1}= 2 n + 3 $ 的两个解分别为 $ x_{1} $,$ x_{2} $($ x_{1} \lt x_{2} $),求 $ \frac{x_{2}-2}{2 x_{1}} $ 的值。

答案： 1. （1）
对于方程$x+\frac{8}{x}=6$，根据材料中$x+\frac{ab}{x}=a + b$的形式，这里$ab = 8$，$a + b = 6$。
由韦达定理可知$x^{2}-6x + 8 = 0$（$x\neq0$，方程$x+\frac{8}{x}=6$两边同乘$x$得到），分解因式得$(x - 2)(x - 4)=0$。
解得$x_{1}=2$，$x_{2}=4$，所以较大的一个解是$4$。
2. （2）
方程$x+\frac{m - n}{mnx}=\frac{m + 4mn - n}{2mn}$两边同乘$mnx$得$mnx^{2}-(\frac{m + 4mn - n}{2})x+(m - n)=0$。
由材料可知$x_{1}x_{2}=\frac{m - n}{mn}$，因为$x_{1}$与$x_{2}$互为倒数，所以$x_{1}x_{2}=1$，即$\frac{m - n}{mn}=1$，$m - n=mn$。
原方程化为$x+\frac{1}{x}=\frac{1 + 4}{2}=\frac{5}{2}$（将$m - n = mn$代入原方程）。
方程两边同乘$2x$得$2x^{2}-5x + 2 = 0$，分解因式得$(2x - 1)(x - 2)=0$。
解得$x_{1}=\frac{1}{2}$，$x_{2}=2$。
3. （3）
对$2x+\frac{n^{2}+2n - 3}{2x - 1}=2n + 3$进行变形：
令$y = 2x - 1$，则$2x=y + 1$，原方程可化为$y + 1+\frac{(n + 3)(n - 1)}{y}=2n + 3$。
即$y+\frac{(n + 3)(n - 1)}{y}=2n + 2$。
由材料可知$y_{1}=n + 3$，$y_{2}=n - 1$（因为$y^{2}-(2n + 2)y+(n + 3)(n - 1)=0$，$y\neq0$）。
当$y = n + 3$时，$2x-1=n + 3$，$x_{2}=\frac{n + 4}{2}$；当$y = n - 1$时，$2x-1=n - 1$，$x_{1}=\frac{n}{2}$。
则$\frac{x_{2}-2}{2x_{1}}=\frac{\frac{n + 4}{2}-2}{2×\frac{n}{2}}=\frac{\frac{n + 4-4}{2}}{n}=\frac{1}{2}$。
综上，（1）答案为$4$；（2）$x_{1}=\frac{1}{2}$，$x_{2}=2$；（3）$\frac{1}{2}$。

21. (10 分)某服装店购进一批甲、乙两种款型时尚 T 恤衫,甲种款型共用了 7800 元,乙种款型共用了 6400 元,其中甲种款型的件数是乙种款型件数的 1.5 倍,甲种款型每件的进价比乙种款型每件的进价少 30 元。
(1)甲、乙两种款型的 T 恤衫各购进了多少件？
(2)该服装店按进价提高 60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,该服装店决定对乙款型按标价的五折降价销售,结果很快全部售完,则售完这批 T 恤衫该服装店共获利多少元？

答案： 1. （1）设乙种款型的$T$恤衫购进$x$件，则甲种款型的$T$恤衫购进$1.5x$件。
根据“甲种款型每件的进价比乙种款型每件的进价少$30$元”列方程：
甲种款型每件进价为$\frac{7800}{1.5x}$元，乙种款型每件进价为$\frac{6400}{x}$元。
则$\frac{6400}{x}-\frac{7800}{1.5x}=30$。
方程两边同乘$1.5x$得：$6400×1.5 - 7800=30×1.5x$。
计算$6400×1.5=9600$，则$9600 - 7800 = 45x$。
即$1800 = 45x$，解得$x = 40$。
经检验，$x = 40$是原方程的解，且符合题意。
那么$1.5x=1.5×40 = 60$（件）。
所以甲种款型的$T$恤衫购进$60$件，乙种款型的$T$恤衫购进$40$件。
2. （2）
甲种款型每件进价：$7800÷60 = 130$（元）。
乙种款型每件进价：$6400÷40 = 160$（元）。
甲款型按进价提高$60\%$标价，则甲款型每件标价：$130×(1 + 60\%)=130×1.6 = 208$（元），甲款型获利：$60×130×60\%=60×78 = 4680$（元）。
乙款型按进价提高$60\%$标价，则乙款型每件标价：$160×(1 + 60\%)=160×1.6 = 256$（元）。
乙款型一半按标价销售，一半按标价的五折销售，乙款型获利：$20×(256 - 160)+20×(256×0.5 - 160)$
先算$20×(256 - 160)=20×96 = 1920$。
再算$256×0.5 = 128$，$20×(128 - 160)=20×(-32)=-640$。
乙款型共获利$1920-640 = 1280$（元）。
售完这批$T$恤衫该服装店共获利：$4680 + 1280=5960$（元）。
综上，（1）甲购进$60$件，乙购进$40$件；（2）共获利$5960$元。

22. (12 分)某市射击队为从甲、乙两名运动员中选拔一人参加省级比赛,对他们进行了四次测试,测试成绩如下表(单位：环)：

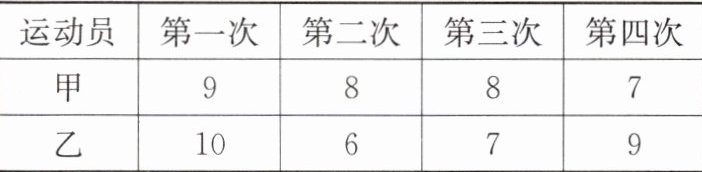
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩；
(2)分别计算甲、乙两人四次测试成绩的方差。
根据计算的结果,你认为推荐谁参加省级比赛更合适？请说明理由。

答案： 1. 计算平均成绩：
甲运动员的平均成绩$\overline{x}_{甲}$：
根据平均数公式$\overline{x}=\frac{x_{1} + x_{2}+\cdots+x_{n}}{n}$（$n = 4$），$\overline{x}_{甲}=\frac{9 + 8+8 + 7}{4}$。
先计算分子$9 + 8+8 + 7=32$，则$\overline{x}_{甲}=\frac{32}{4}=8$（环）。
乙运动员的平均成绩$\overline{x}_{乙}$：
同样根据平均数公式，$\overline{x}_{乙}=\frac{10 + 6+7 + 9}{4}$。
先计算分子$10 + 6+7 + 9=32$，则$\overline{x}_{乙}=\frac{32}{4}=8$（环）。
2. 计算方差：
方差公式$s^{2}=\frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots+(x_{n}-\overline{x})^{2}]$。
甲运动员成绩的方差$s_{甲}^{2}$：
$s_{甲}^{2}=\frac{1}{4}[(9 - 8)^{2}+(8 - 8)^{2}+(8 - 8)^{2}+(7 - 8)^{2}]$。
先计算各项$(9 - 8)^{2}=1$，$(8 - 8)^{2}=0$，$(8 - 8)^{2}=0$，$(7 - 8)^{2}=1$。
则$s_{甲}^{2}=\frac{1}{4}(1 + 0+0 + 1)=\frac{1}{4}×2 = 0.5$。
乙运动员成绩的方差$s_{乙}^{2}$：
$s_{乙}^{2}=\frac{1}{4}[(10 - 8)^{2}+(6 - 8)^{2}+(7 - 8)^{2}+(9 - 8)^{2}]$。
先计算各项$(10 - 8)^{2}=4$，$(6 - 8)^{2}=4$，$(7 - 8)^{2}=1$，$(9 - 8)^{2}=1$。
则$s_{乙}^{2}=\frac{1}{4}(4 + 4+1 + 1)=\frac{1}{4}×10 = 2.5$。
3. 推荐人选：
因为$\overline{x}_{甲}=\overline{x}_{乙}=8$，说明两人的平均水平相当。
又因为$s_{甲}^{2}＜s_{乙}^{2}$，根据方差的意义，方差越小，数据越稳定。
所以推荐甲参加省级比赛更合适。
综上，（1）$\overline{x}_{甲}=8$环，$\overline{x}_{乙}=8$环；（2）$s_{甲}^{2}=0.5$，$s_{乙}^{2}=2.5$，推荐甲参加省级比赛更合适，理由是甲、乙平均成绩相同，但甲的成绩更稳定。