《2025年同步练习册山东科学技术出版社八年级数学上册鲁教版五四制》

1. 某校为了丰富学生的课余活动,开展了一次歌咏比赛,共有18名同学入围,他们的决赛成绩如下表：

则入围同学决赛成绩的极差是(A)
A.0.5
B.9.60
C.9.40
D.9.90

答案： A

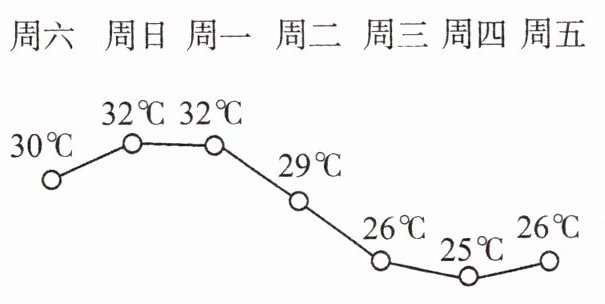
2. 下面是某地未来7日最高气温走势图,这组数据的极差为7℃.

答案： 7

3. 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩都是9.4环,方差分别是$s_{甲}^{2}= 0.90$,$s_{乙}^{2}= 1.22$,$s_{丙}^{2}= 0.43$,$s_{丁}^{2}= 1.68$. 在本次射击测试中,成绩最稳定的是(C)
A.甲
B.乙
C.丙
D.丁

答案： C

4. 若一组数据3,5,6,2,x,7,0的众数是5,则这组数据的方差是$\frac{36}{7}$.

答案： $\frac{36}{7}$

例1 已知样本数据1,2,3,4,5,求这个样本的：
(1)平均数$\overline{x}$；
(2)方差$s^{2}$.

答案： 【点拨】
(1)根据平均数的公式计算即可.
(2)根据方差公式$s^{2}= \frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+…+(x_{n}-\overline{x})^{2}]$进行计算即可.
【解】
(1)$\overline{x}= \frac{1}{5}(1+2+3+4+5)= 3$.
(2)$s^{2}= \frac{1}{5}[(1-3)^{2}+(2-3)^{2}+(3-3)^{2}+(4-3)^{2}+(5-3)^{2}]= 2$.

例2 甲、乙两台机床同时加工直径为100mm的零件,为了检验产品的质量,从加工的产品中各随机抽出6件进行测量,测得数据如下(单位：mm)：
甲机床：99 100 98 100 100 103
乙机床：99 100 102 99 100 100
(1)分别计算上述两组数据的平均数及方差；
(2)根据(1)中的计算结果,哪一台机床加工这种零件更符合要求?

答案： 【点拨】
(1)根据平均数的公式和方差的公式求解即可.

(2)方差反映了一组数据的波动程度,方差越大,波动性越大,故方差小的机床加工这种零件更符合要求.
【解】
(1)$\overline{x}_{甲}= 100+\frac{1}{6}(-1+0-2+0+0+3)= 100$,
$\overline{x}_{乙}= 100+\frac{1}{6}(-1+0+2-1+0+0)= 100$.
$s_{甲}^{2}= \frac{1}{6}[(99-100)^{2}+(100-100)^{2}+(98-100)^{2}+(100-100)^{2}+(100-100)^{2}+(103-100)^{2}]= \frac{1}{6}(1+0+4+0+0+9)= \frac{7}{3}$,
$s_{乙}^{2}= \frac{1}{6}[(99-100)^{2}+(100-100)^{2}+(102-100)^{2}+(99-100)^{2}+(100-100)^{2}+(100-100)^{2}]= \frac{1}{6}(1+0+4+1+0+0)= 1$.

(2)由
(1)可知,$\overline{x}_{甲}= \overline{x}_{乙}$,而$s_{甲}^{2}＞s_{乙}^{2}$,

∴乙机床加工这种零件更符合要求.