第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
例 2 某社区调查居民双休日的学习情况,采取下列调查方式:A. 从一幢高层住宅楼中选取 200 名居民;B. 从不同住宅楼中随机选取 200 名居民;C. 选取社区内的 200 名在校学生.
(1)上述调查方式最合理的是(
(2)将最合理的调查方式得到的数据绘制成以下扇形统计图和频数分布直方图.
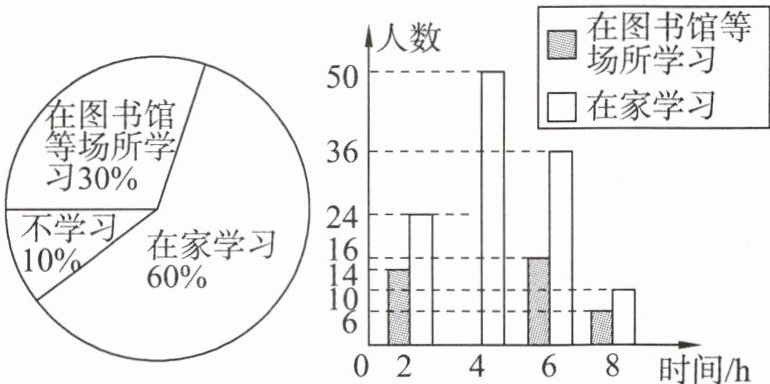
①请补全频数分布直方图;
②在这次调查的 200 名居民中,“在家学习”的有
③“不学习”所对的扇形的圆心角是
(3)请估计该社区 2 000 名居民中双休日学习时间不少于 4 h 的人数.
(1)上述调查方式最合理的是(
B
);(填序号)(2)将最合理的调查方式得到的数据绘制成以下扇形统计图和频数分布直方图.

①请补全频数分布直方图;
②在这次调查的 200 名居民中,“在家学习”的有
120
人;③“不学习”所对的扇形的圆心角是
36°
;(3)请估计该社区 2 000 名居民中双休日学习时间不少于 4 h 的人数.
$\frac{24 + 50 + 16 + 36 + 6 + 10}{200}×2000 = 1420$(人)
答:估计该社区$2000$名居民中双休日学习时间不少于$4h$的人数为$1420$人。
答:估计该社区$2000$名居民中双休日学习时间不少于$4h$的人数为$1420$人。
答案:
【点拨】
(1)抽样调查时,为了获得较为准确的调查结果,要注意样本的代表性和广泛性.
(2)①先求出在图书馆等场所学习的总人数,再求出在图书馆等场所学习 4 h 的人数,然后补全统计图即可;
②利用 200 名居民中“在家学习”的占 60%即可求出答案;
③用 $360^{\circ}$乘以“不学习”所占的百分比即可求出圆心角的度数.
(3)首先利用频数分布直方图中的有关数据,计算出双休日学习时间不少于 4 h 的人数占样本的百分比,然后利用样本估计总体,从而算出该社区 2 000 名居民中双休日学习时间不少于 4 h 的人数.
【解】
(1)调查方式最合理的是 B.
(2)①$200×30\% - 14 - 16 - 6 = 24$,补充图形如图所示.

②在家学习的有 $200×60\% = 120$(人).
③$360^{\circ}×10\% = 36^{\circ}$.
(3)根据题意得
$\frac{24 + 50 + 16 + 36 + 6 + 10}{200}×2 000 = 1 420$(人).
答:估计该社区 2 000 名居民中双休日学习时间不少于 4 h 的人数为 1 420 人.
【点拨】
(1)抽样调查时,为了获得较为准确的调查结果,要注意样本的代表性和广泛性.
(2)①先求出在图书馆等场所学习的总人数,再求出在图书馆等场所学习 4 h 的人数,然后补全统计图即可;
②利用 200 名居民中“在家学习”的占 60%即可求出答案;
③用 $360^{\circ}$乘以“不学习”所占的百分比即可求出圆心角的度数.
(3)首先利用频数分布直方图中的有关数据,计算出双休日学习时间不少于 4 h 的人数占样本的百分比,然后利用样本估计总体,从而算出该社区 2 000 名居民中双休日学习时间不少于 4 h 的人数.
【解】
(1)调查方式最合理的是 B.
(2)①$200×30\% - 14 - 16 - 6 = 24$,补充图形如图所示.

②在家学习的有 $200×60\% = 120$(人).
③$360^{\circ}×10\% = 36^{\circ}$.
(3)根据题意得
$\frac{24 + 50 + 16 + 36 + 6 + 10}{200}×2 000 = 1 420$(人).
答:估计该社区 2 000 名居民中双休日学习时间不少于 4 h 的人数为 1 420 人.
查看更多完整答案,请扫码查看


