第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图,在四边形 ABCD 中,对角线 AC 平分∠BAD,AB>AD,下列结论正确的是(
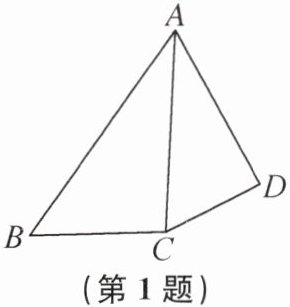
A.AB-AD>CB-CD
B.AB-AD= CB-CD
C.AB-AD<CB-CD
D.AB-AD 与 CB-CD 的大小关系不确定
A
)
A.AB-AD>CB-CD
B.AB-AD= CB-CD
C.AB-AD<CB-CD
D.AB-AD 与 CB-CD 的大小关系不确定
答案:
A 提示:在AB上截取AE=AD,连接CE.易证△AEC≌△ADC,所以CE=CD,所以AB - AD = AB - AE = BE.根据三角形三边之间的关系,可知BE > CB - CE = CB - CD,即AB - AD > CB - CD.
2. 如图,BD 是∠ABC 的平分线,AD⊥BD,垂足为 D.若∠DAC= 15°,∠C= 50°,则∠BAD 的度数为(
A.35°
B.45°
C.55°
D.65°
D
)A.35°
B.45°
C.55°
D.65°
答案:
D 提示:延长AD交BC于点E.根据外角的性质,可知∠BED = ∠DAC + ∠C = 65°.易证△BAD≌△BED,所以∠BAD = ∠BED = 65°.
3. 如图,点 E 在正方形 ABCD 的对角线上,且 EC= 2AE,直角三角形 FEG 的两直角边 EF,EG 分别交边 BC,DC 于点 M,N.若正方形 ABCD 的边长为a,则重叠部分四边形 EMCN 的面积为(
A.$\frac{2}{3}a^{2}$
B.$\frac{1}{4}a^{2}$
C.$\frac{5}{9}a^{2}$
D.$\frac{4}{9}a^{2}$
D
)A.$\frac{2}{3}a^{2}$
B.$\frac{1}{4}a^{2}$
C.$\frac{5}{9}a^{2}$
D.$\frac{4}{9}a^{2}$
答案:
D 提示:如图,过点E分别作EP⊥BC于点P,EQ⊥CD于点Q.因为四边形ABCD是正方形,所以∠BCD = 90°.又因为∠EPM = ∠EQN = 90°,所以∠PEQ = 90°,所以∠PEM + ∠MEQ = 90°.因为△FEG是直角三角形,所以∠NEF = ∠QEN + ∠MEQ = 90°,所以∠PEM = ∠QEN.因为AC是∠BCD的平分线,EP⊥BC,EQ⊥CD,所以EP = EQ,所以四边形PCQE是正方形,△EPM≌△EQN(ASA),所以S△EPM = S△EQN,所以S四边形EMCN = S△EQN + S四边形EMCQ = S△EPM + S四边形EMCQ = S正方形PCQE.因为正方形ABCD的边长为a,所以AC = √2a.因为EC = 2AE,所以EC = 2√2/3a,所以EP = PC = 2/3a,所以S正方形PCQE = 2/3a·2/3a = 4/9a².
4. 如图,在△ABC 中,AC= BC,∠ACB= 90°,D 是边 AB 的中点,点 E 在边 AC 上,点 F 在边 BC 上,DE⊥DF,AE= 4,BF= 3,则 EF 的长为(
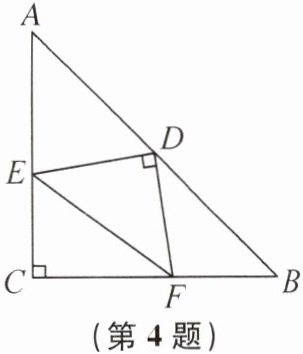
A.4
B.5
C.6
D.7
B
)
A.4
B.5
C.6
D.7
答案:
B 提示:连接CD.因为AC = BC,∠ACB = 90°,所以△ABC是等腰直角三角形,所以∠A = ∠B = 45°.因为D为边AB的中点,所以CD = AD,CD平分∠BCA,CD⊥AB,所以∠DCF = 45°.因为DE⊥DF,所以∠CDF + ∠EDC = 90°.因为∠ADE + ∠EDC = 90°,所以∠ADE = ∠CDF.易证△ADE≌△CDF,所以CF = AE = 4.所以AC = BC = BF + CF = 7,所以CE = AC - AE = 3.在Rt△CEF中,由勾股定理,得EF = √(CE² + CF²) = 5.
5. 如图,等边三角形 ABC 的边长为 8 cm,点 P 从点 C 出发,以 1 cm/s 的速度向点 B 匀速运动,同时点 Q 也从点 C 出发,以 2 cm/s 的速度向点 A 匀速运动,AP,BQ 交于点 M,当点 Q 到达点 A 时,P,Q 两点停止运动.设 P,Q 两点运动的时间为 t s.若∠AMQ= 60°,则 t 的值是(
A.1
B.2
C.$\frac{8}{3}$
D.3
C
)A.1
B.2
C.$\frac{8}{3}$
D.3
答案:
C 提示:由条件,得AC = AB = 8cm,∠BAC = ∠C = 60°.根据题意,得CP = t cm,CQ = 2t cm,所以AQ = (8 - 2t)cm.因为∠ABQ + ∠BAP = ∠AMQ = 60°,∠CAP + ∠BAP = ∠BAC = 60°,所以∠ABQ = ∠CAP.易证△ABQ≌△CAP,所以AQ = CP,即8 - 2t = t,解得t = 8/3.
6. 如图,在五边形 ABCDE 中,∠ABC= ∠AED= 90°,AB= CD= AE= BC+DE= 2,则五边形 ABCDE 的面积为______
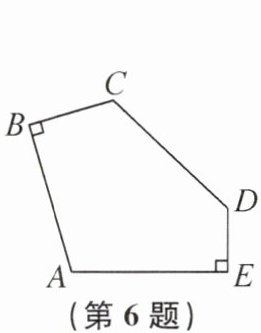
4
.
答案:
4 提示:延长DE至点F,使EF = BC,连接AC,AD,AF.因为AB = CD = AE = BC + DE,∠ABC = ∠AED = 90°,由题中条件,可得Rt△ABC≌Rt△AEF,△ACD≌△AFD,所以S五边形ABCDE = 2S△ADF = 2×1/2DF·AE = 4.
7. 如图,在四边形 ABCD 中,∠ABC= ∠ADC= 90°,AB= CB,连接 AC,BD.若 BD= 7 cm,则$S_{四边形ABCD}= $
$\frac{49}{2}$
$cm^{2}$.
答案:
49/2 提示:延长DC至点E,使CE = AD,连接BE.因为∠ABC = ∠ADC = 90°,所以∠BAD + ∠BCD = 360° - ∠ABC - ∠ADC = 180°.因为∠BCD + ∠BCE = 180°,所以∠BAD = ∠BCE.易证△ABD≌△CBE,所以BE = BD = 7cm,S△ABD = S△CBE,∠ABD = ∠CBE.因为∠ABC = ∠ABD + ∠DBC = 90°,所以∠CBE + ∠DBC = ∠DBE = 90°.所以S四边形ABCD = S△BDE = 1/2BD·BE = 49/2cm².
8. 如图,在四边形 ABCD 中,AC,BD 为对角线,△ABC 为等边三角形,∠ADC= 30°,AD= 2,BD= 3,则 CD 的长为______.
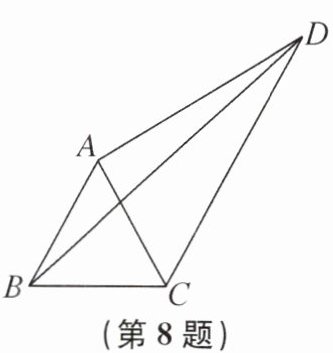

答案:
√5 提示:以CD为边向右侧作等边三角形CDE,连接AE,则∠ADE = 90°.由条件,易证△ACE≌△BCD,所以AE = BD.在Rt△ADE中,根据勾股定理,得DE = √(AE² - AD²) = √(BD² - AD²) = √5,所以CD = DE = √5.
查看更多完整答案,请扫码查看


