《2025年小题狂做八年级数学上册苏科版提优版》

1.(2025 南京市联合体期末)下列各组数中,是勾股数的是(B)
A.$1,\sqrt{3},2$
B.5,12,13
C.6,7,8
D.8,24,25

答案： B

2.(2025 南京市玄武区期末)在$\triangle ABC$中,$\angle A,\angle B,\angle C的对应边分别是a,b,c$.下列条件中,不能判断$\triangle ABC$是直角三角形的是(D)
A.$c^{2}= a^{2}-b^{2}$
B.$a:b:c= 3:4:5$
C.$\angle C= \angle B-\angle A$
D.$\angle A:\angle B:\angle C= 3:4:5$

答案： D

3. 如图,下列四个三角形中各有一边长为 6,一边长为 8.若第三边长分别为 6,8,10,12,则面积最大的三角形是(C)

答案： C 提示:作出每一个三角形中长度为8的边上的高，根据垂线段最短可知，选项A、B、D中，长度为8的边上的高都小于6；选项C中，由$6^{2}+8^{2}=10^{2}$可知，该三角形为直角三角形，所以长度为8的边上的高为6，故选项C的面积最大。

4. 如图,在四边形$ABCD$中,$AD\perp AB$,$AD= AB= \sqrt{2}$,$BC= \sqrt{5}$,$DC= 1$,则$\angle ADC$的度数是$135^{\circ}$.

答案： $135^{\circ}$ 提示:连接BD。因为$\angle A = 90^{\circ}$，$AD = AB = \sqrt{2}$，所以$\angle ADB = 45^{\circ}$。在$Rt\triangle ADB$中，$BD^{2}=AD^{2}+AB^{2}=4$。在$\triangle CDB$中，$CB^{2}-DC^{2}=(\sqrt{5})^{2}-1^{2}=4$。所以$CB^{2}-DC^{2}=BD^{2}$，即$CB^{2}=DC^{2}+BD^{2}$，所以$\angle CDB = 90^{\circ}$，所以$\angle ADC = \angle ADB + \angle CDB = 135^{\circ}$。

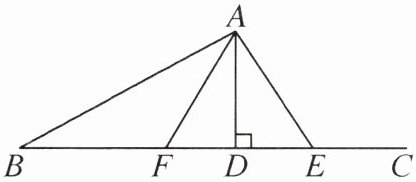
5. 如图,$AD\perp BC$,垂足为$D$,且$AD= 4$,$BD= 8$.点$E从点B沿射线BC$方向以每秒 2 个单位长度的速度匀速运动,$F为BE$的中点,连接$AE$,$AF$,设点$E运动的时间为t\ \text{s}$.
(1)当$t$为何值时,$AE= AF$？
(2)当$t= 5$时,判断$\triangle ABE$的形状,并说明理由.
]

答案： 解:
(1)由题意，得$BE = 2t$，且当$AE = AF$时，点F在点D左侧。因为F为BE的中点，所以$BF = EF = \frac{1}{2}BE = t$。因为$AD = 4$，$BD = 8$，所以$DF = BD - BF = 8 - t$，$DE = BE - BD = 2t - 8$。因为$AD\perp BC$，所以$\angle ADB = \angle ADE = 90^{\circ}$。在$Rt\triangle ADF$中，$AF^{2}=AD^{2}+DF^{2}=16+(8 - t)^{2}$。在$Rt\triangle ADE$中，$AE^{2}=AD^{2}+DE^{2}=16+(2t - 8)^{2}$，所以$16+(8 - t)^{2}=16+(2t - 8)^{2}$，解得$t = \frac{16}{3}$或$t = 0$（舍去）。所以当$t = \frac{16}{3}$时，$AE = AF$。
(2)$\triangle ABE$是直角三角形。理由如下:当$t = 5$时，$BE = 2t = 10$，所以$DE = BE - BD = 2$。在$Rt\triangle ADB$中，$AB^{2}=AD^{2}+BD^{2}=80$。在$Rt\triangle ADE$中，$AE^{2}=AD^{2}+DE^{2}=20$。因为$AB^{2}+AE^{2}=100$，$BE^{2}=10^{2}=100$，所以$AB^{2}+AE^{2}=BE^{2}$，所以$\triangle ABE$是直角三角形。

6. 小明在学习完本节课后,对勾股定理的逆定理的证明提出了新的方法,以下是他作业本上的证明过程：
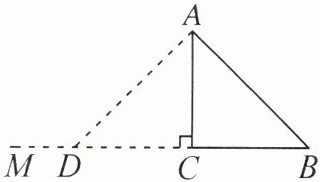
已知：如图,在$\triangle ABC$中,$AC^{2}+BC^{2}= AB^{2}$.
求证：$\triangle ABC$是直角三角形.
证明：作$CM\perp AC$,垂足为$C$,在$CM上截取CD= BC$,连接$AD$.因为$\angle ACD= 90^{\circ}$,所以$AC^{2}+CD^{2}= AD^{2}$.因为$AC^{2}+BC^{2}= AB^{2}$,$CD= BC$,所以$AD^{2}= AB^{2}$,所以$AD= AB$,即$\triangle ADB$是等腰三角形.所以$AC\perp DB$,所以$\triangle ABC$是直角三角形.
(1)阅读上述小明的证明过程,用笔画出其中错误的步骤.
(2)按照小明添加的辅助线方法,修正小明的证明过程.
]

答案： 解:
(1)错误的步骤为“所以$AD = AB$。即$\triangle ADB$是等腰三角形”。提示:因为图中D、C、B三点是否共线并未说明，所以由$AD = AB$得不到$\triangle ADB$是等腰三角形。
(2)修正证明过程如下:作$CM\perp AC$，垂足为C，在CM上截取$CD = BC$，连接AD。因为$\angle ACD = 90^{\circ}$，所以$AC^{2}+CD^{2}=AD^{2}$。因为$AC^{2}+BC^{2}=AB^{2}$，$CD = BC$，所以$AD^{2}=AB^{2}$，所以$AD = AB$。在$\triangle ACD$和$\triangle ACB$中，$\begin{cases}DC = BC\\AC = AC\\AD = AB\end{cases}$，所以$\triangle ACD\cong\triangle ACB(SSS)$，所以$\angle ACB = \angle ACD = 90^{\circ}$，所以$\triangle ACB$是直角三角形。