《2025年小题狂做八年级数学上册苏科版提优版》

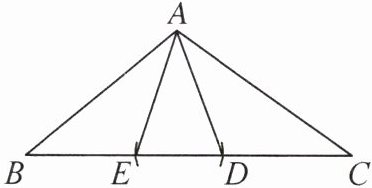
1. (2024 无锡市宜兴市期中)如图,在△ABC中,以点 B 为圆心,AB 长为半径画弧,交边 BC 于点 D,以点 C 为圆心,AC 长为半径画弧,交边 BC 于点 E. 若∠B= 40°,∠C= 36°,则关于 AD,AE,BE,CD 的大小关系正确的是 (D)

A.AD= AE
B.AD＜AE
C.BE= CD
D.BE＜CD

答案： D　提示:因为∠C＜∠B，所以AB＜AC.因为AB = BD，AC = EC，所以BD＜EC，即BE + ED＜ED + CD，所以BE＜CD.

2. 同一平面内有5个点,每3个点都不在同一条直线上,以其中任意3点组成的三角形共有 ( )

A.3个
B.5个
C.8个
D.10个

答案：
D　提示:如图，一共能组成10个三角形，分别是△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,△BCD,△BCE,△BDE,△CDE.

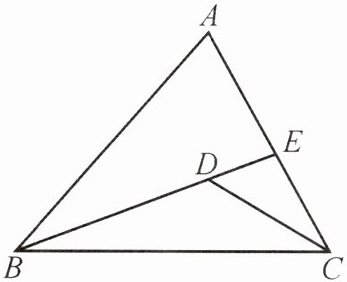
3. 如图,若把有一条公共边的两个三角形称为一对"共边三角形",则图中以 BC 为公共边的"共边三角形"有 (B)

A.2对
B.3对
C.4对
D.6对

答案： B　提示:根据题意，得以BC为公共边的“共边三角形”有△BDC与△BEC,△BDC与△BAC,△BEC与△BAC,共3对.

4. 下列长度的三条线段与长度为5的线段首尾依次相连能组成四边形的是 (D)
A.1,1,1
B.1,1,8
C.1,2,2
D.2,2,2

答案： D　提示:因为1 + 1 + 1 = 3＜5，所以此三条线段与长度为5的线段不能组成四边形，故选项A不符合题意；因为1 + 1 + 5 = 7＜8，所以此三条线段与长度为5的线段不能组成四边形，故选项B不符合题意；因为1 + 2 + 2 = 5，所以此三条线段与长度为5 的线段不能组成四边形，故选项C不符合题意；因为2 + 2 + 2 = 6＞5，所以此三条线段与长度为5的线段能组成四边形，故选项D符合题意.

5. 已知三角形的三条边长均为整数,其中有一边长为4,但不是最短边,则这样的三角形共有8个.

答案： 8　提示:因为4不是最短边，所以分为两类:当4是中间边时，有(2,4,5),(3,4,5),(3,4,6)；当4是最长边时，有(1,4,4),(2,3,4),(2,4,4),(3,3,4),(3,4,4)，综上所述，共有8个.

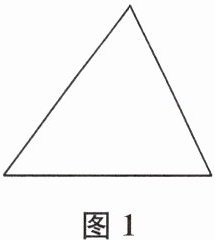
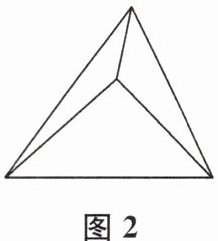
6. (2024 苏州市姑苏区期中)如图,图1中有1个三角形,在图1中的三角形内部(不含边界)取一点,连接该点与三角形的3个顶点得到图2,图2中共有4个三角形.若在图2中的一个小三角形内部(不含边界)取一点,连接该点与该小三角形的3个顶点得到图3.在虚线框中画出图3,图3中共有7或9个三角形.(写出所有可能的值)

答案： 7或9　提示:共有两种情况:①如图1,两点不在同一直线上，分别连接三个顶点，共有7个三角形；②如图2,两点在同一直线上，分别连接三个顶点，共有9个三角形.

7. 已知a,b,c是一个三角形三条边的长.
(1) 小明认为"代数式|a+b-c|+|b-a-c|-|a-c+b|的值总是正数",小明的看法对吗?请说明理由.
(2) 取一组你喜欢的a,b,c的整数值,并求出(1)中代数式的值.

答案： 解:
(1)小明的看法是对的.理由如下:根据三角形的三边关系，得a + b＞c，a + c＞b，所以原式=(a + b - c)+(-b + a + c)-(a - c + b)=a - b + c.因为a + c＞b，所以a - b + c＞0.所以代数式|a + b - c|+|b - a - c|-|a - c + b|的值总是正数，即小明的看法是对的.
(2)答案不唯一.例如:a = 2，b = 3，c = 4，则a - b + c = 2 - 3 + 4 = 3，所以原代数式的值为3.

8. 如图,P 为△ABC 内任意一点,试说明:AB+AC＞PB+PC.

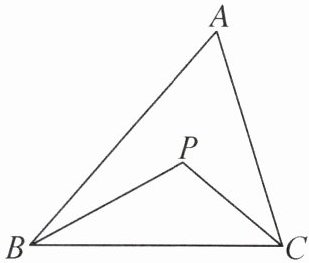
答案： 解:延长BP交AC于点D.根据三角形的三边关系，得AB + AD＞BD，CD + PD＞PC，所以AB + AD + CD + PD＞BD + PC，即AB + AC + PD＞BP + PD + PC.所以AB + AC＞PB + PC.