第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
8. 如图,点E,F在线段CD上,且AC//DB,AE//BF,AE= BF.求证:△AED≌△BFC.

证明:

证明:
答案:
证明:因为AC//DB,AE//BF,所以∠ACE=∠BDF,∠AEC=∠BFD.又因为AE=BF,所以△AEC≌△BFD (AAS),所以CE=DF,所以CF=DE.因为∠AEC=∠BFD,所以∠AED=∠BFC.所以△AED≌△BFC(SAS).
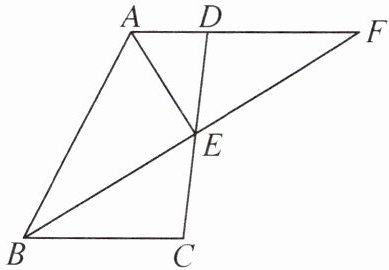
9. 如图,已知AD//BC,E是CD上一点,BF平分∠ABC,交AD的延长线于点F,且AE⊥BF.
(1)求证:△ABE≌△AFE.
(2)若AD= 3,BC= 8,求AB的长.
(1)求证:△ABE≌△AFE.
(2)若AD= 3,BC= 8,求AB的长.

答案:
(1)证明:因为AE⊥BF,所以∠BEA=∠FEA=90°.因为BF平分∠ABC,所以∠ABE=∠CBE.因为AD//BC,所以∠CBE=∠F,所以∠ABE=∠F.又因为AE=AE,所以△ABE≌△AFE(AAS).
(2)解:因为△ABE≌△AFE,所以BE=FE,AB=AF.在△BCE和△FDE中,
∠CBE=∠F,
BE=FE,所以△BCE≌△FDE(ASA),
∠BEC=∠FED,
所以BC=FD,所以AB=AF=AD+FD=AD+BC=11.
(1)证明:因为AE⊥BF,所以∠BEA=∠FEA=90°.因为BF平分∠ABC,所以∠ABE=∠CBE.因为AD//BC,所以∠CBE=∠F,所以∠ABE=∠F.又因为AE=AE,所以△ABE≌△AFE(AAS).
(2)解:因为△ABE≌△AFE,所以BE=FE,AB=AF.在△BCE和△FDE中,
∠CBE=∠F,
BE=FE,所以△BCE≌△FDE(ASA),
∠BEC=∠FED,
所以BC=FD,所以AB=AF=AD+FD=AD+BC=11.
1. 利用基本作图不能作出唯一三角形的条件是(
A.已知三边
B.已知两边及其夹角
C.已知两角及一边
D.已知两边及其中一边的对角
D
)A.已知三边
B.已知两边及其夹角
C.已知两角及一边
D.已知两边及其中一边的对角
答案:
D
2. 如图,AC与DB交于点O,下列条件不能证明△ABC≌△DCB的是(
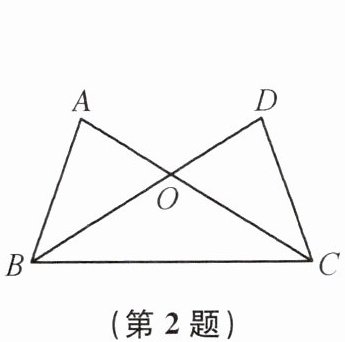
A.AB= DC,AC= DB
B.∠A= ∠D,∠ABC= ∠DCB
C.BO= CO,∠A= ∠D
D.AB= DC,∠ACB= ∠DBC
D
)
A.AB= DC,AC= DB
B.∠A= ∠D,∠ABC= ∠DCB
C.BO= CO,∠A= ∠D
D.AB= DC,∠ACB= ∠DBC
答案:
D
3. 如图,AB= AC,点D,E分别在AC,AB上,且AE= AD,连接EC,BD,相交于点M,连接AM,则下列结论错误的是(
A.△EBM≌△DCM
B.若S△BEM= S△ADM,则E是AB的中点
C.MA平分∠EMD
D.若E是AB的中点,则BM+AC<EM+BD
D
)A.△EBM≌△DCM
B.若S△BEM= S△ADM,则E是AB的中点
C.MA平分∠EMD
D.若E是AB的中点,则BM+AC<EM+BD
答案:
D 提示:因为AB=AC,∠BAD=∠CAE,AD=AE,所以△ABD≌△ACE(SAS),所以∠B=∠C,BD=CE.因为AB=AC,AE=AD,所以AB - AE=AC - AD,所以BE=CD.又因为∠B=∠C,∠EMB=∠DMC,所以△EBM≌△DCM(AAS),故选项A正确.所以ME=MD,又因为AE=AD,AM=AM,所以△AEM≌△ADM(SSS),所以∠AME=∠AMD,$S_{\triangle AEM}=S_{\triangle ADM}$,所以MA平分∠EMD,故选项C正确.若$S_{\triangle BEM}=S_{\triangle ADM}$,则$S_{\triangle BEM}=S_{\triangle AEM}$,所以ME为△AMB的中线,所以E为AB的中点,故选项B正确.延长ME至点N,使得EN=EM,连接AN.若E是AB的中点,则AE=BE.又因为EN=EM,∠AEN=∠BEM,所以△ANE≌△BME(SAS),所以AN=BM.又因为BD=CE,所以BM+AC=AN+AC>CN=EN+CE=EM+BD,即BM+AC>EM+BD,故选项D错误.
4. 如图,在△ABC中,∠ACB= 90°,AC= 8 cm,BC= 12 cm,点P从点A出发沿A→C→B路径向终点B运动;点Q从点B出发沿B→C→A路径向终点A运动.点P和点Q分别以1 cm/s和3 cm/s的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P,Q作PE⊥l于点E,QF⊥l于点F.当点P运动
2或5或16
s时,△PEC与△QFC全等.
答案:
2或5或16 提示:因为PE⊥l于点E,QF⊥l于点F,所以∠PEC=∠CFQ=90°,所以∠QCF+∠CQF=90°.①如图1,当0≤t<4时,点P在边AC上,点Q在边BC上.此时有AP=t cm,BQ=3t cm.因为∠ACB=90°,所以∠PCE+∠QCF=90°,所以∠PCE=∠CQF.易知当PC=QC时,△PEC≌△CFQ,此时8 - t=12 - 3t,解得t=2.②如图2,当4≤t<$\frac{20}{3}$时,点P,Q在边AC上.易知当PC=QC时,△PEC≌△QFC,此时8 - t=3t - 12,解得t=5.③当$\frac{20}{3}$≤t<8时,点Q停在点A处,点P在边AC上,此时△PEC与△QFC不全等.④如图3,当8≤t<20时,点Q停在点A处,点P在边BC上.同①可得∠PCE=∠CQF,所以当PC=QC=8,即t - 8=8时,△PEC≌△CFQ,解得t=16.综上所述,当t的值为2或5或16时,△PEC与△QFC全等.
5. 如图,AD//BC,AB//CD,AE⊥AD,AF⊥AB,且AE= AB,AF= AD.求证:AC= EF.

证明:

证明:
答案:
证明:因为AD//BC,AB//CD,所以∠DAC=∠BCA,∠BAC=∠DCA.又因为AC=CA,所以△ADC≌△CBA (ASA),所以AD=CB.又因为AF=AD,所以AF=CB.因为AD//BC,所以∠DAB+∠ABC=180°.因为AE⊥AD,AF⊥AB,所以∠DAE=∠BAF=90°,所以∠EAF+∠DAB=180°,所以∠EAF=∠ABC.在△EAF和△ABC中,因为AE=BA,∠EAF=∠ABC,AF=BC,所以△EAF≌△ABC(SAS),所以AC=EF.
查看更多完整答案,请扫码查看


