第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
2. 如图,三个正比例函数的图象分别对应表达式:①$y= ax$,②$y= bx$,③$y= cx$,将$a$,$b,c$从小到大排列为 (
A.$a<b<c$
B.$a<c<b$
C.$b<a<c$
D.$c<b<a$
B
)A.$a<b<c$
B.$a<c<b$
C.$b<a<c$
D.$c<b<a$
答案:
B 提示:根据三个函数图象所在象限,可得a<0,b>0,c>0,再根据直线越陡,|k|越大,得b>c.所以a<c<b.
3. 已知点$A(n,n+2),B(n-1,n+4),C(m,t)$是正比例函数图象上的三个点,当$m>3$时,$t$的取值范围是
t<-6
.
答案:
t<-6 提示:设正比例函数表达式为y=kx.将点A(n,n+2),B(n-1,n+4)代入,得$\left\{\begin{array}{l}nk=n+2,\\ (n-1)k=n+4,\end{array}\right.$解得k=-2,所以正比例函数的表达式为y=-2x.因为-2<0,所以y随x的增大而减小.当m=3时,y=-6.因为点C(m,t)是正比例函数图象上的点,所以当m>3时,t<-6.
4. 如图,直线$l_{1}⊥x轴于点(1,0)$,直线$l_{2}⊥x轴于点(2,0)$,直线$l_{3}⊥x轴于点(3,0)$……直线$l_{n}⊥x轴于点(n,0)$.函数$y= x的图象与直线l_{1},l_{2},l_{3},…,l_{n}分别交于点A_{1},A_{2},A_{3},…,A_{n}$;函数$y= 3x的图象与直线l_{1},l_{2},l_{3},…,l_{n}分别交于点B_{1},B_{2},B_{3},…,B_{n}$.如果$\triangle OA_{1}B_{1}的面积记作S_{1}$,$\triangle OA_{2}B_{2}的面积记作S_{2}$,$\triangle OA_{3}B_{3}的面积记作S_{3}$……$\triangle OA_{n}B_{n}的面积记作S_{n}$,那么$S_{20}= $
400
.
答案:
400
5. 已知函数$y= x,y= -2x,y= \frac{1}{2}x,y= 3x$.
(1) 画出每个函数的图象.
【探索发现】
(2) 观察这些函数的图象可以发现,随$|k|$的增大,直线与$y$轴的位置关系有何变化?
【灵活运用】
(3) 如图2,已知正比例函数$y_{1}= k_{1}x,y_{2}= k_{2}x$在同一平面直角坐标系中,则$k_{1}与k_{2}$的大小关系为______.
]

(1) 画出每个函数的图象.
【探索发现】
(2) 观察这些函数的图象可以发现,随$|k|$的增大,直线与$y$轴的位置关系有何变化?
【灵活运用】
(3) 如图2,已知正比例函数$y_{1}= k_{1}x,y_{2}= k_{2}x$在同一平面直角坐标系中,则$k_{1}与k_{2}$的大小关系为______.
]


答案:
解:
(1)函数图象如图所示.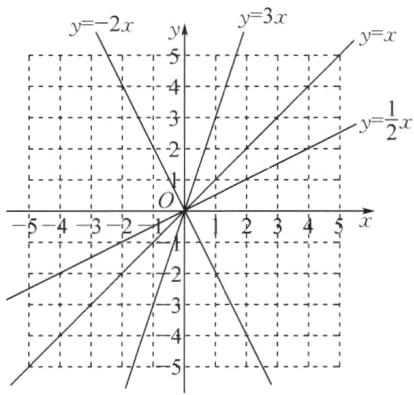
(2)观察这些函数的图象可以发现,随|k|的增大直线与y轴的夹角越小.
(3)k₁>k₂ 提示:由
(2)得,|k₁|<|k₂|.因为k₁<0,k₂<0,所以k₁>k₂.
解:
(1)函数图象如图所示.

(2)观察这些函数的图象可以发现,随|k|的增大直线与y轴的夹角越小.
(3)k₁>k₂ 提示:由
(2)得,|k₁|<|k₂|.因为k₁<0,k₂<0,所以k₁>k₂.
6. 数学课上,老师要求同学们画函数$y= |x|$的图象,小红联想绝对值的性质得$y= x$ ($x≥0$)或$y= -x(x≤0)$,于是她很快画出了该函数的图象(如图).
(1) 小红所作的图对吗? 如果不对,请你画出正确的函数图象.
(2) 根据上述的作图方法,请画出函数$y= -3|x|$的图象.

(1) 小红所作的图对吗? 如果不对,请你画出正确的函数图象.
(2) 根据上述的作图方法,请画出函数$y= -3|x|$的图象.

答案:
解:
(1)不对.y=|x|=$\left\{\begin{array}{l}x(x>0),\\ -x(x≤0),\end{array}\right.$函数图象如图1所示.
(2)函数y=-3|x|的图象如图2所示.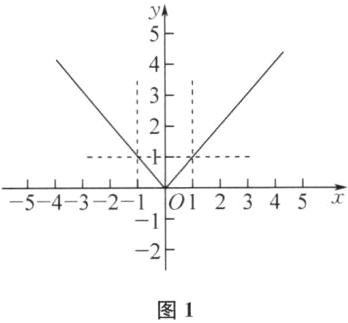

解:
(1)不对.y=|x|=$\left\{\begin{array}{l}x(x>0),\\ -x(x≤0),\end{array}\right.$函数图象如图1所示.
(2)函数y=-3|x|的图象如图2所示.


查看更多完整答案,请扫码查看


