第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC 为0.7 m,梯子顶端到地面的距离AC为2.4 m. 如果保持梯子底端位置不动,将梯子斜靠在右墙,那么梯子顶端到地面的距离A'D 为1.5 m. 由以上信息可知小巷的宽为(
A.2 m
B.2.5 m
C.2.6 m
D.2.7 m
D
)A.2 m
B.2.5 m
C.2.6 m
D.2.7 m
答案:
D
2. 如图,某人到岛上去探宝,从点A处登陆后先往北走9 km,又往东走6 km,再向北走3 km,最后往西走1 km就找到宝藏,则登陆点A与宝藏埋藏点B之间的距离是(
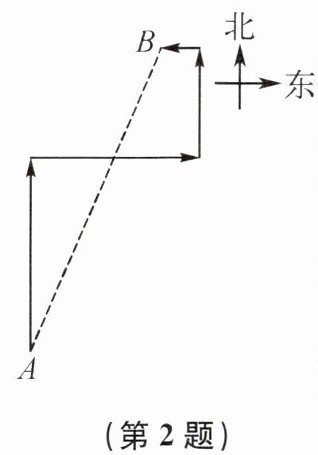
A.10 km
B.11 km
C.12 km
D.13 km
D
)
A.10 km
B.11 km
C.12 km
D.13 km
答案:
D
3. 一艘海轮以每小时24海里的速度从港口A出发向东南方向航行,另一艘海轮以每小时18海里的速度同时从港口A出发向西南方向航行,则离开港口2 h后,两艘海轮之间的距离为(
A.84海里
B.60海里
C.48海里
D.36海里
B
)A.84海里
B.60海里
C.48海里
D.36海里
答案:
B
4. 如图,点A是正方体左侧面的中心,B是正方体的一个顶点,正方体的棱长为2,一只蚂蚁从点A沿其表面爬到点B的最短路程是
$\sqrt{10}$
.
答案:
$\sqrt{10}$ 提示:正方体的部分展开图如图所示.过点A作$AE\perp CD$于点E,连接AB,则AB的长为最短路程.因为四棱柱为正方体,所以$DC=BC=2$,$AD=AC$.又因为$AE\perp DC$,所以$DE=EC$,$AE=EC=\frac{1}{2}DC=1$,所以$BE=EC+BC=3$.在$\text{Rt}\triangle AEB$中,根据勾股定理,得$AB=\sqrt{AE^2+BE^2}=\sqrt{10}$.
5.(2025南京市建邺区期末)如图,把摆钟的摆锤看作一个点,当它摆动到最低点D处时,摆锤离底座的垂直高度DE= 5 cm,当它摆动到最高点B处时,摆锤离底座的垂直高度BF= 7 cm,且与摆锤在最低点D处时的水平距离BC= 10 cm,求钟摆AD的长度.
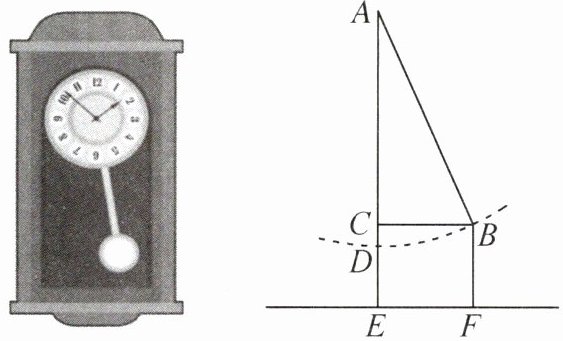

答案:
解:由题意,得$CD=CE - DE=2\ \text{cm}$.设$AD=AB=x\ \text{cm}$,则$AC=AD - CD=(x - 2)\ \text{cm}$.因为$\angle ACB=90^\circ$,所以$AB^2=AC^2+BC^2$,即$x^2=(x - 2)^2+10^2$,解得$x=26$.答:钟摆AD的长度为26 cm.
6. 同学们想测量旗杆的高度,他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学应用勾股定理分别提出解决这个问题的方案如下:
小明:①如图1,测量出绳子垂直落地后还剩余1 m;②如图2,把绳子拉直,绳子末端在地面上离旗杆底部的距离AC= 4 m.
小亮:如图3,先在旗杆底端的绳子上打一个结,然后举起绳结拉到点D处(BD= BC),过点D作DF⊥AC于点F,DF= EC.
(1)请你按小明的方案求出旗杆的高度BC.
(2)已知小亮举起绳结离旗杆的距离DE= 4.5 m,求此时绳结到地面的高度DF.
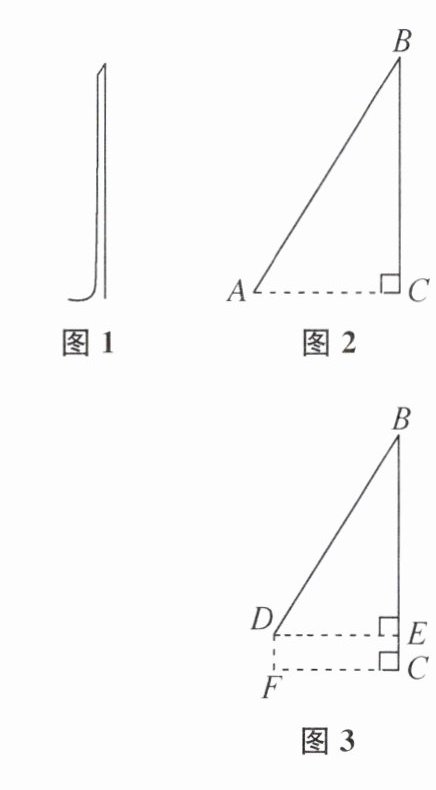
小明:①如图1,测量出绳子垂直落地后还剩余1 m;②如图2,把绳子拉直,绳子末端在地面上离旗杆底部的距离AC= 4 m.
小亮:如图3,先在旗杆底端的绳子上打一个结,然后举起绳结拉到点D处(BD= BC),过点D作DF⊥AC于点F,DF= EC.
(1)请你按小明的方案求出旗杆的高度BC.
(2)已知小亮举起绳结离旗杆的距离DE= 4.5 m,求此时绳结到地面的高度DF.

答案:
(1)设旗杆的高度BC为$x\ \text{m}$,则绳子的长度$AB=(x + 1)\ \text{m}$.在$\text{Rt}\triangle ABC$中,由勾股定理,得$x^2+4^2=(x + 1)^2$,解得$x=7.5$.答:旗杆的高度BC为7.5 m.
(2)由
(1)可知,$BD=BC=7.5\ \text{m}$.在$\text{Rt}\triangle BDE$中,由勾股定理,得$BE=\sqrt{BD^2-DE^2}=\sqrt{7.5^2-4.5^2}=6(\text{m})$,所以$DF=EC=BC - BE=1.5\ \text{m}$.答:此时绳结到地面的高度DF为1.5 m.
(1)设旗杆的高度BC为$x\ \text{m}$,则绳子的长度$AB=(x + 1)\ \text{m}$.在$\text{Rt}\triangle ABC$中,由勾股定理,得$x^2+4^2=(x + 1)^2$,解得$x=7.5$.答:旗杆的高度BC为7.5 m.
(2)由
(1)可知,$BD=BC=7.5\ \text{m}$.在$\text{Rt}\triangle BDE$中,由勾股定理,得$BE=\sqrt{BD^2-DE^2}=\sqrt{7.5^2-4.5^2}=6(\text{m})$,所以$DF=EC=BC - BE=1.5\ \text{m}$.答:此时绳结到地面的高度DF为1.5 m.
查看更多完整答案,请扫码查看


