第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.有下列说法:①买2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买1件乙家的售价约为3元.其中正确的说法是 (

A.①②
B.②③④
C.②③
D.①②③
D
)
A.①②
B.②③④
C.②③
D.①②③
答案:
D
2. 一个装有进水管和出水管的容器,开始时,先打开进水管注水;3 min时,再打开出水管排水;8 min时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量 y(L)与时间 x(min)之间的函数关系如图所示,则图中a的值为
$\frac{29}{3}$
.
答案:
$\frac{29}{3}$
3. 如图1,一个正方体铁块放置在圆柱形水槽内.现以一定的速度往水槽中注水,28 s时注满水槽.水槽内水面的高度 y(cm)与注水时间 x(s)之间的函数图象如图2所示.
(1)正方体的棱长为
(2)求线段AB对应的函数表达式,并写出自变量x的取值范围.
(3)如果将正方体铁块取出,又经过t s恰好将此水槽注满,请直接写出t的值.
(1)正方体的棱长为
10
cm.(2)求线段AB对应的函数表达式,并写出自变量x的取值范围.
线段AB对应的函数表达式为$y = \frac{5}{8}x+\frac{5}{2}$,自变量x的取值范围是$12\leqslant x\leqslant28$。
(3)如果将正方体铁块取出,又经过t s恰好将此水槽注满,请直接写出t的值.
4
答案:
【解析】:
(1)根据图2可知,12s时水面高度达到$10cm$,此后水面上升速度变慢,说明此时水已淹没正方体。
因为正方体底面积为边长的平方,水面高度达到$10cm$时刚好淹没正方体,所以正方体棱长为$10cm$。
(2)设线段$AB$对应的函数表达式为$y = kx + b$($k\neq0$)。
已知$A(12,10)$,$B(28,20)$,将这两点代入$y = kx + b$中,可得方程组$\begin{cases}12k + b = 10\\28k + b = 20\end{cases}$。
用第二个方程减去第一个方程消去$b$可得:
$28k + b -(12k + b)=20 - 10$,
$28k + b - 12k - b = 10$,
$16k = 10$,
解得$k=\frac{5}{8}$。
将$k=\frac{5}{8}$代入$12k + b = 10$可得:
$12×\frac{5}{8}+b = 10$,
$\frac{15}{2}+b = 10$,
$b = 10 - \frac{15}{2}=\frac{5}{2}$。
所以线段$AB$对应的函数表达式为$y=\frac{5}{8}x+\frac{5}{2}$,自变量$x$的取值范围是$12\leq x\leq28$。
(3)在没有正方体时,注满水槽需$12+(28 - 12)÷(1-\frac{正方体底面积}{圆柱底面积})$。
由图可知,$12s$时水刚好淹没正方体,$28s$注满,有正方体时$16s$水面上升了$20 - 10 = 10cm$。
设圆柱底面积为$S$,正方体底面积为$10×10 = 100cm^2$,则$\frac{20}{S×28 - 100×(28 - 12)}=\frac{10}{S×16 - 100×(16 - 12)}$,
$\frac{20}{28S - 1600}=\frac{10}{16S - 400}$,
$20×(16S - 400)=10×(28S - 1600)$,
$320S - 8000 = 280S - 16000$,
$320S - 280S=-16000 + 8000$,
$40S=-8000$,
解得$S = 200cm^2$。
那么没有正方体时,注满水槽的时间为$12+\frac{16×(200 - 100)}{200}=12 + 8 = 20s$。
已经注水$28s$,所以$t = 20-(28 - 12)=4s$。
【答案】:
(1)$10$;
(2)$y=\frac{5}{8}x+\frac{5}{2}(12\leq x\leq28)$;
(3)$4$。
(1)根据图2可知,12s时水面高度达到$10cm$,此后水面上升速度变慢,说明此时水已淹没正方体。
因为正方体底面积为边长的平方,水面高度达到$10cm$时刚好淹没正方体,所以正方体棱长为$10cm$。
(2)设线段$AB$对应的函数表达式为$y = kx + b$($k\neq0$)。
已知$A(12,10)$,$B(28,20)$,将这两点代入$y = kx + b$中,可得方程组$\begin{cases}12k + b = 10\\28k + b = 20\end{cases}$。
用第二个方程减去第一个方程消去$b$可得:
$28k + b -(12k + b)=20 - 10$,
$28k + b - 12k - b = 10$,
$16k = 10$,
解得$k=\frac{5}{8}$。
将$k=\frac{5}{8}$代入$12k + b = 10$可得:
$12×\frac{5}{8}+b = 10$,
$\frac{15}{2}+b = 10$,
$b = 10 - \frac{15}{2}=\frac{5}{2}$。
所以线段$AB$对应的函数表达式为$y=\frac{5}{8}x+\frac{5}{2}$,自变量$x$的取值范围是$12\leq x\leq28$。
(3)在没有正方体时,注满水槽需$12+(28 - 12)÷(1-\frac{正方体底面积}{圆柱底面积})$。
由图可知,$12s$时水刚好淹没正方体,$28s$注满,有正方体时$16s$水面上升了$20 - 10 = 10cm$。
设圆柱底面积为$S$,正方体底面积为$10×10 = 100cm^2$,则$\frac{20}{S×28 - 100×(28 - 12)}=\frac{10}{S×16 - 100×(16 - 12)}$,
$\frac{20}{28S - 1600}=\frac{10}{16S - 400}$,
$20×(16S - 400)=10×(28S - 1600)$,
$320S - 8000 = 280S - 16000$,
$320S - 280S=-16000 + 8000$,
$40S=-8000$,
解得$S = 200cm^2$。
那么没有正方体时,注满水槽的时间为$12+\frac{16×(200 - 100)}{200}=12 + 8 = 20s$。
已经注水$28s$,所以$t = 20-(28 - 12)=4s$。
【答案】:
(1)$10$;
(2)$y=\frac{5}{8}x+\frac{5}{2}(12\leq x\leq28)$;
(3)$4$。
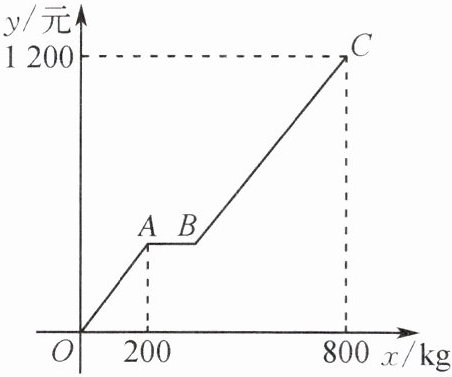
4. 某商店代理销售一种水果,6月份的销售利润 y(元)与销售量 x(kg)之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下列问题.
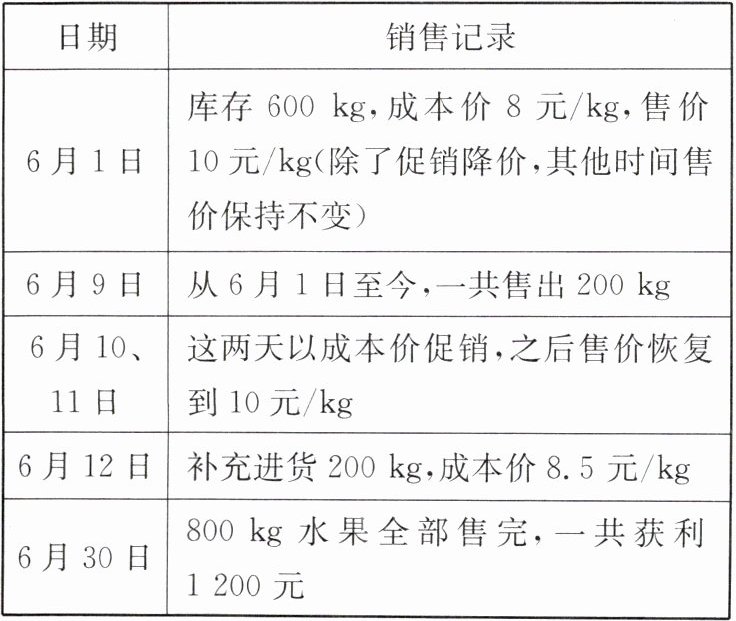
|日期|销售记录|
|6月1日|库存600 kg,成本价8元/kg,售价10元/kg(除了促销降价,其他时间售价保持不变)|
|6月9日|从6月1日至今,一共售出200 kg|
|6月10、11日|这两天以成本价促销,之后售价恢复到10元/kg|
|6月12日|补充进货200 kg,成本价8.5元/kg|
|6月30日|800 kg水果全部售完,一共获利1200元|
(1)截至6月9日,该商店销售这种水果一共获利多少元?
(2)求图象中线段BC所在直线对应的函数表达式.
|日期|销售记录|
|6月1日|库存600 kg,成本价8元/kg,售价10元/kg(除了促销降价,其他时间售价保持不变)|
|6月9日|从6月1日至今,一共售出200 kg|
|6月10、11日|这两天以成本价促销,之后售价恢复到10元/kg|
|6月12日|补充进货200 kg,成本价8.5元/kg|
|6月30日|800 kg水果全部售完,一共获利1200元|

(1)截至6月9日,该商店销售这种水果一共获利多少元?
(2)求图象中线段BC所在直线对应的函数表达式.

答案:
(1)截至6月9日,该商店销售这种水果一共获利$200×(10-8)=400$(元).
(2)设点 B 的坐标为$(a,400)$.根据题意,得$(10-8)×(600-a)+(10-8.5)×200=1200-400$,解得$a=350$.所以点 B的坐标为$(350,400)$.设线段 BC 所在直线的函数表达式为$y=kx+b(k≠0)$.因为B,C 两点的坐标分别为$(350,400),(800,1200)$,所以$\left\{\begin{array}{l} 350k+b=400,\\ 800k+b=1200,\end{array}\right. $解得$\left\{\begin{array}{l} k=\frac {16}{9},\\ b=-\frac {2000}{9}.\end{array}\right. $所以线段 BC 所在直线的函数表达式为$y=\frac {16}{9}x-\frac {2000}{9}.$
(1)截至6月9日,该商店销售这种水果一共获利$200×(10-8)=400$(元).
(2)设点 B 的坐标为$(a,400)$.根据题意,得$(10-8)×(600-a)+(10-8.5)×200=1200-400$,解得$a=350$.所以点 B的坐标为$(350,400)$.设线段 BC 所在直线的函数表达式为$y=kx+b(k≠0)$.因为B,C 两点的坐标分别为$(350,400),(800,1200)$,所以$\left\{\begin{array}{l} 350k+b=400,\\ 800k+b=1200,\end{array}\right. $解得$\left\{\begin{array}{l} k=\frac {16}{9},\\ b=-\frac {2000}{9}.\end{array}\right. $所以线段 BC 所在直线的函数表达式为$y=\frac {16}{9}x-\frac {2000}{9}.$
查看更多完整答案,请扫码查看


