第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
2. $(-\sqrt{2})^{2}$的平方根是 (
A.-1.414
B.$\pm 1.414$
C.$\sqrt{2}$
D.$\pm \sqrt{2}$
D
)A.-1.414
B.$\pm 1.414$
C.$\sqrt{2}$
D.$\pm \sqrt{2}$
答案:
D
3. 若方程$(x-5)^{2}= 19的两根为a和b$,且$a>b$,则下列结论正确的是 (
A.$a$是 19 的算术平方根
B.$b$是 19 的平方根
C.$a-5$是 19 的算术平方根
D.$b+5$是 19 的平方根
C
)A.$a$是 19 的算术平方根
B.$b$是 19 的平方根
C.$a-5$是 19 的算术平方根
D.$b+5$是 19 的平方根
答案:
C
4. 有下列五个命题:①只有正数才有平方根;②-2 是 4 的平方根;③5 的平方根是$\sqrt{5}$;④$\pm \sqrt{3}$都是 3 的平方根;⑤$(-2)^{2}$的平方根是-2.其中正确的命题是 (
A.①②③
B.③④⑤
C.③④
D.②④
D
)A.①②③
B.③④⑤
C.③④
D.②④
答案:
D
5. 观察下表中的数据信息.
|$x$|15|15.1|15.2|15.3|15.4|15.5|
|$x^{2}$|225|228.01|231.04|234.09|237.16|240.25|
|$x$|15.6|15.7|15.8|15.9|16|
|$x^{2}$|243.36|246.49|249.64|252.81|256|
根据表中的信息判断,下列说法正确的是 (
A.$\sqrt{2.3409}= 1.53$
B.247 的算术平方根比 15.7 小
C.根据表中数据的变化趋势,可以推断出$14.9^{2}$比 225 小 3.01
D.只有 3 个正整数$n满足15.9\leq \sqrt{n}\leq 16$
|$x$|15|15.1|15.2|15.3|15.4|15.5|
|$x^{2}$|225|228.01|231.04|234.09|237.16|240.25|
|$x$|15.6|15.7|15.8|15.9|16|
|$x^{2}$|243.36|246.49|249.64|252.81|256|
根据表中的信息判断,下列说法正确的是 (
A
)A.$\sqrt{2.3409}= 1.53$
B.247 的算术平方根比 15.7 小
C.根据表中数据的变化趋势,可以推断出$14.9^{2}$比 225 小 3.01
D.只有 3 个正整数$n满足15.9\leq \sqrt{n}\leq 16$
答案:
A
6. 若一个正数的平方根是$2a+1$和$-a-4$,则这个正数是
49
.
答案:
49 提示:由题意,得$2a+1-a-4=0$,解得$a=3$.所以$2a+1=7$,所以这个正数为$7^{2}=49$.
7. 若$(x-3)^{2}= 2$,则$x= $
$3\pm\sqrt{2}$
.
答案:
$3\pm\sqrt{2}$
8. 观察与思考:
因为$11^{2}= 121$,所以$\pm \sqrt{121}= \pm 11$;
因为$111^{2}= 12321$,所以$\pm \sqrt{12321}= \pm 111$;
……
由此猜想:$\pm \sqrt{12345678987654321}= $
因为$11^{2}= 121$,所以$\pm \sqrt{121}= \pm 11$;
因为$111^{2}= 12321$,所以$\pm \sqrt{12321}= \pm 111$;
……
由此猜想:$\pm \sqrt{12345678987654321}= $
±111 111 111
.
答案:
±111 111 111
9. 已知$a,b$均为正整数,如果$0<\sqrt{a}-b<1$,我们称$b是\sqrt{a}$ 的"主要值",那么$\sqrt{37}$的"主要值"是
6
.
答案:
6 提示:$0<\sqrt{a}-b<1$,所以$b<\sqrt{a}<b+1$.因为$\sqrt{36}<\sqrt{37}<\sqrt{49}$,所以$6<\sqrt{37}<7$,所以$b=6$.
10. 若一个正数两个平方根之差为$a(a>0)$,则这个正数是
$\frac{a^{2}}{4}$
.
答案:
$\frac{a^{2}}{4}$
11. 已知$a是\sqrt{16}$的平方根,$b= \sqrt{9}$,则$a+b$的值为
5或1
.
答案:
5或1 提示:因为$\sqrt{16}=4$,所以$a=\pm2$.又因为$b=\sqrt{9}=3$,所以当$a=2$时,$a+b=2+3=5$;当$a=-2$时,$a+b=-2+3=1$.
12. 求下列各式中$x$的值:
(1)$\frac{x^{2}}{2}-98= 0$;
(2)$4(x+1)^{2}= 81$.
(1)$\frac{x^{2}}{2}-98= 0$;
(2)$4(x+1)^{2}= 81$.
答案:
解:
(1)因为$\frac{x^{2}}{2}-98=0$,所以$\frac{x^{2}}{2}=98$,所以$x^{2}=196$,解得$x=\pm14$.
(2)因为$4(x+1)^{2}=81$,所以$x+1=\pm\frac{9}{2}$,所以$x=-1+\frac{9}{2}=\frac{7}{2}$或$x=-1-\frac{9}{2}=-\frac{11}{2}$.
(1)因为$\frac{x^{2}}{2}-98=0$,所以$\frac{x^{2}}{2}=98$,所以$x^{2}=196$,解得$x=\pm14$.
(2)因为$4(x+1)^{2}=81$,所以$x+1=\pm\frac{9}{2}$,所以$x=-1+\frac{9}{2}=\frac{7}{2}$或$x=-1-\frac{9}{2}=-\frac{11}{2}$.
13. 已知$\sqrt{x-y+3}与\sqrt{x+y-1}$互为相反数,求$(x-y)^{2}$的平方根.
答案:
解:因为$\sqrt{x-y+3}$与$\sqrt{x+y-1}$互为相反数,所以$\sqrt{x-y+3}+\sqrt{x+y-1}=0$,所以$\begin{cases} x-y+3=0, \\ x+y-1=0, \end{cases}$解得$\begin{cases} x=-1, \\ y=2. \end{cases}$所以$(x-y)^{2}=9$,所以$(x-y)^{2}$的平方根是±3.
14. 已知$a$在数轴上对应的位置如图所示,试化简:$\pm \sqrt{(2a-1)^{2}}+|a+1|$.
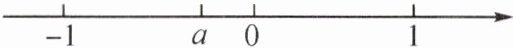
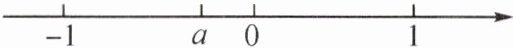
答案:
解:由数轴,可知$-1<a<0$,从而可得$|a+1|=a+1$,所以$\pm\sqrt{(2a-1)^{2}}+|a+1|=\pm(2a-1)+(a+1)$,结果为$2-a$或$3a$.
查看更多完整答案,请扫码查看


