《2025年小题狂做八年级数学上册苏科版提优版》

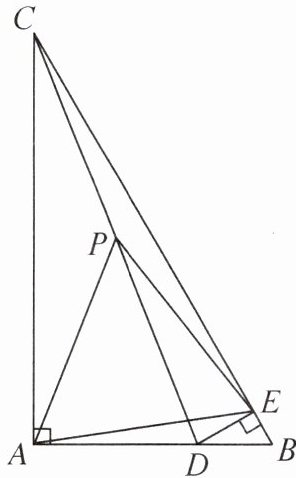
8. 如图,在Rt△ABC中,∠CAB= 90°,∠ACB= 30°,D是边AB上一点(不与点A,B重合),DE⊥BC于点E.若P是CD的中点,请判断△PAE的形状,并说明理由.

答案： 解:△PAE为等边三角形.理由如下:因为在Rt△CAD中,∠CAD=90°,P是斜边CD的中点,所以PA=PC=$\frac{1}{2}$CD,所以∠ACD=∠PAC,所以∠APD=∠ACD+∠PAC=2∠ACD.同理可得,在Rt△CED中,PE=PC=$\frac{1}{2}$CD,∠DPE=2∠DCB,所以PA=PE,∠APE=∠APD+∠DPE=2∠ACD+2∠DCB=2∠ACB=60°,所以△PAE是等边三角形.

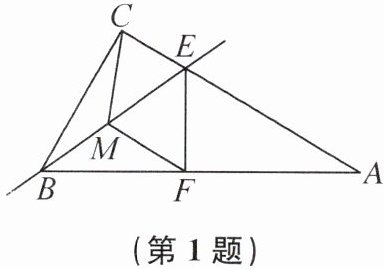
1. 如图,在Rt△ABC中,∠ACB= 90°,E是边AC上的动点(不与点A,C重合).设M为线段BE的中点,过点E作EF⊥AB,垂足为F,连接MC,MF.若∠CBA= 50°,则在点E运动过程中,∠CMF的度数(B)

A.等于80°
B.等于100°
C.等于130°
D.无法确定

答案： B 提示:根据“直角三角形斜边上的中线等于斜边的一半”可得MC=MB=ME,MF=MB=ME,所以∠CME=∠CBM+∠BCM=2∠CBM,∠FME=2∠FBM,所以∠CMF=2∠CBA=100°.

2. 如图,∠ABC= 60°,AB= 6,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动.设点P的运动时间为t s,当△ABP为锐角三角形时,t的取值范围是3＜t＜12.

答案： 3＜t＜12 提示:当∠APB=90°时,∠BAP=30°,所以BP=$\frac{1}{2}$AB=3;当∠BAP=90°时,∠APB=30°,所以BP=2AB=12,所以当3＜BP＜12,即3＜t＜12时,△ABP为锐角三角形.

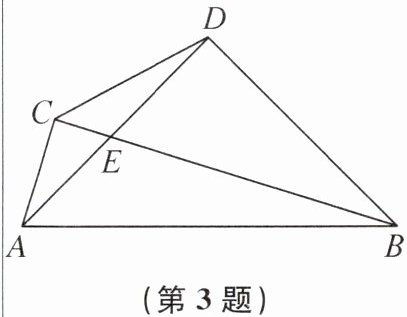
3. 如图,在以AB为斜边的Rt△ABD和Rt△ABC中,∠ACB= ∠ADB= 90°,CD= m,AB= 2m,则∠AEB= ______.

答案：
120° 提示:如图,取AB的中点F,连接CF,DF.因为∠ACB=∠ADB=90°,所以CF=$\frac{1}{2}$AB=DF.又因为CD=m,AB=2m,所以CD=$\frac{1}{2}$AB,所以CF=DF=CD,所以△CDF是等边三角形,所以∠CFD=60°,所以∠AFC+∠BFD=120°.因为CF=BF,AF=DF,所以∠AFC=2∠ABE,∠BFD=2∠BAE,即∠ABE=$\frac{1}{2}$∠AFC,∠BAE=$\frac{1}{2}$∠BFD.所以∠ABE+∠BAE=$\frac{1}{2}$(∠AFC+∠BFD)=$\frac{1}{2}$×120°=60°,所以∠AEB=180°−60°=120°.

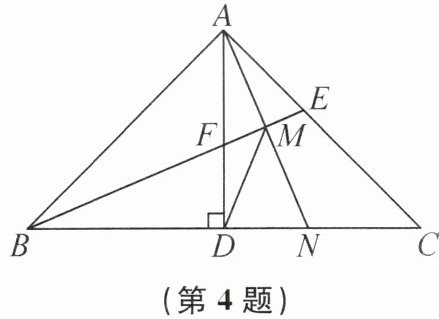
4. 如图,在等腰直角三角形ABC中,∠BAC= 90°,AD⊥BC于点D,∠ABC的平分线分别交AC,AD于点E,F,M为EF的中点,AM的延长线交BC于点N,连接DM.现有下列结论:①DF= DN;②△DMN为等腰三角形;③MD平分∠BMN;④AE= NC.其中正确的结论是______①②③④(填序号).

答案： ①②③④ 提示:由条件,得∠C=∠ABC=45°,∠CBE=∠ABE=22.5°,所以∠AEF=∠C+∠CBE=67.5°,∠AFE=∠DFB=90°−∠CBE=67.5°,所以△AFE是等腰三角形,因为M为EF的中点,所以AM⊥EF,所以∠BAN=∠BNA=67.5°,所以△ABN是等腰三角形,又因为BE平分∠ABC,所以M为AN的中点,因为AD⊥BC,所以DM=MN,所以△DMN为等腰三角形,故②正确;因为BM⊥AN,所以∠DAN+∠AFM=90°,又因为∠FBD+∠BFD=90°,∠BFD=∠AFM,所以∠FBD=∠DAN,易证△BFD≌△AND,所以DF=DN,故①正确;因为△DMN为等腰三角形,∠BNA=67.5°,所以∠MDN=∠MND=67.5°,所以∠DMN=45°,所以MD平分∠BMN,故③正确;由题条件可知AD=DC,又因为DF=DN,所以AF=CN,又因为AF=AE,所以AE=CN,故④正确.

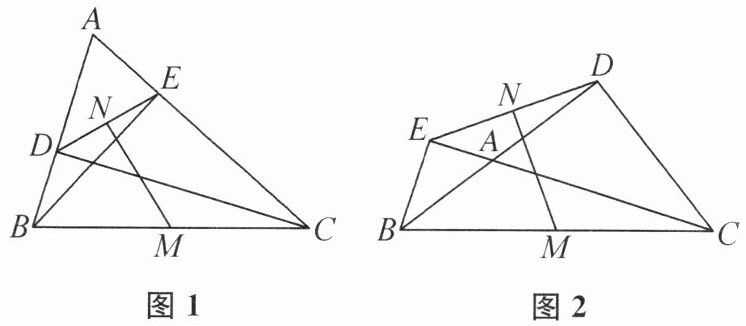
5. 如图1,在锐角三角形ABC中,CD,BE分别是边AB,AC上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,试猜想∠A与∠DME之间的关系,并证明你的猜想.
(3)如图2,当∠BAC变为钝角时,(1)(2)中的结论是否都成立?若结论成立,请直接回答,不需证明;若结论不成立,请说明理由.

答案：
(1)证明:连接DM,ME.因为CD,BE分别是边AB,AC上的高,M是BC的中点,所以DM=$\frac{1}{2}$BC,ME=$\frac{1}{2}$BC,所以DM=ME.又因为N是DE的中点,所以MN⊥DE.
(2)解:∠DME=180° - 2∠A.证明如下:在△ABC中,∠ABC+∠ACB=180° - ∠A.因为DM=ME=BM=MC,所以∠BMD+∠CME=(180° - 2∠ABC)+(180° - 2∠ACB)=360° - 2(∠ABC+∠ACB)=360° - 2(180° - ∠A)=2∠A,所以∠DME=180° - 2∠A.
(3)解:结论
(1)成立,结论
(2)不成立.理由如下:连接DM,ME.同
(1),易证MN⊥DE,故
(1)中结论成立.在△ABC中,∠ABC+∠ACB=180° - ∠BAC.因为DM=ME=BM=MC,所以∠BME+∠CMD=2∠ACB+2∠ABC=2(180° - ∠BAC)=360° - 2∠BAC,所以∠DME=180°-(360° - 2∠BAC)=2∠BAC - 180°.故
(2)中结论不成立.