第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. (2024 泰州市兴化市期中)在正方形网格中,∠AOB 的位置如图所示,到∠AOB 两边距离相等的点应是 (

A.点 M
B.点 N
C.点 P
D.点 Q
A
)
A.点 M
B.点 N
C.点 P
D.点 Q
答案:
A
2. 如图,已知 AP,CP 分别是△ABC 的外角∠DAC,∠ECA 的平分线,PM⊥BD,PN⊥BE,垂足分别为 M,N,则 PM 与 PN 的关系是 (
A.PM>PN
B.PM= PN
C.PM<PN
D.无法确定
B
)A.PM>PN
B.PM= PN
C.PM<PN
D.无法确定
答案:
B
3. 如图,有三条两两相交的公路$ l_1,l_2,l_3. $现在要建一个加油站,使它到三条公路的距离相等,那么加油站可建的地点有______个.


答案:
4 提示:如图,加油站可建的地点有4个.
4 提示:如图,加油站可建的地点有4个.

4. 如图,点 A,C 分别在射线 BE,BF 上,连接 AC,∠ABC,∠EAC 的平分线 BP,AP 交于点 P,过点 P 分别作 PM⊥BE,PN⊥BF,垂足为 M,N. 给出下列结论:①CP 平分∠ACF;②∠ABC+2∠APC= 180°;③∠ACB= 2∠APB;④S△PAC= S△MAP+S△NCP. 其中正确的结论是______
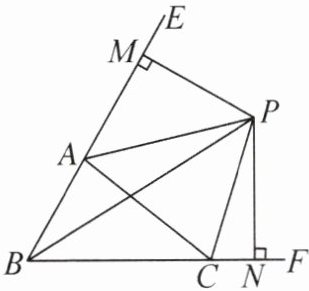
①②③④
(填序号).
答案:
①②③④ 提示:过点P作PD⊥AC于点D.因为PB平分∠ABC,PA平分∠EAC,PM⊥BE,PN⊥BF,PD⊥AC,所以PM=PN,PM=PD,所以PN=PD,所以点P在∠ACF的平分线上,故①正确.因为PM⊥AB,PN⊥BC,所以∠ABC+90°+∠MPN+90°=360°,所以∠ABC+∠MPN=180°.易证Rt△PAM≌Rt△PAD,Rt△PCD≌Rt△PCN,所以∠APM=∠APD,∠CPD=∠CPN,所以∠MPN=2∠APC,所以∠ABC+2∠APC=180°,故②正确.因为PA平分∠CAE,BP平分∠ABC,所以2∠PAM=∠CAE=∠ABC+∠ACB,∠PAM=∠ABP+∠APB=$\frac{1}{2}$∠ABC+∠APB,所以∠ACB=2∠APB,故③正确.由②可知Rt△PAM≌Rt△PAD(HL),Rt△PCD≌Rt△PCN(HL),所以S△PAM=S△PAD,S△PCD=S△PCN,所以S△PAM+S△PCN=S△PAD+S△PCD=S△PAC,故④正确.
5. 如图,在∠AOB 的两边 OA,OB 上分别取点 M,N,连接 MN. 若 MP 平分∠AMN,NP 平分∠MNB.
(1) 求证:OP 平分∠AOB.
(2) 若 MN= 8,且△PMN 与△OMN 的面积分别是 16 和 24,求线段 OM 与 ON 的长度之和.
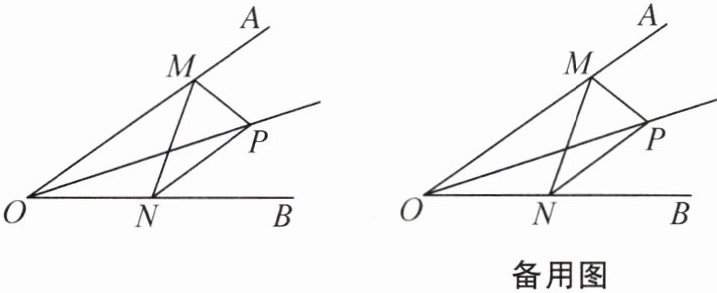
(1) 求证:OP 平分∠AOB.
(2) 若 MN= 8,且△PMN 与△OMN 的面积分别是 16 和 24,求线段 OM 与 ON 的长度之和.

答案:
(1)证明:如图,过点P分别作PC⊥OA于点C,PD⊥MN于点D,PE⊥OB于点E.因为MP平分∠AMN,PC⊥OA,PD⊥MN,所以PC=PD.因为NP平分∠MNB,PD⊥MN,PE⊥OB,所以PD=PE,所以PC=PE,所以OP平分∠AOB.
(2)解:因为S△PMN=16,即$\frac{1}{2}$MN·PD=16,所以PD=4,所以PC=PE=PD=4.因为S△OMN=24,所以S△POM+S△PON=S四边形MONP=S△PMN+S△OMN=40,即$\frac{1}{2}$OM·PC+$\frac{1}{2}$ON·PE=40,所以OM+ON=20,即线段OM与ON的长度之和为20.
(1)证明:如图,过点P分别作PC⊥OA于点C,PD⊥MN于点D,PE⊥OB于点E.因为MP平分∠AMN,PC⊥OA,PD⊥MN,所以PC=PD.因为NP平分∠MNB,PD⊥MN,PE⊥OB,所以PD=PE,所以PC=PE,所以OP平分∠AOB.

(2)解:因为S△PMN=16,即$\frac{1}{2}$MN·PD=16,所以PD=4,所以PC=PE=PD=4.因为S△OMN=24,所以S△POM+S△PON=S四边形MONP=S△PMN+S△OMN=40,即$\frac{1}{2}$OM·PC+$\frac{1}{2}$ON·PE=40,所以OM+ON=20,即线段OM与ON的长度之和为20.
查看更多完整答案,请扫码查看


