第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 若5y+2与x-3成正比例,则y是x的(
A.正比例函数
B.一次函数
C.没有函数关系
D.以上答案都不正确
B
)A.正比例函数
B.一次函数
C.没有函数关系
D.以上答案都不正确
答案:
B
2. 当x= 5时,一次函数y= 2x+k和y= 3kx-4(k≠0)的值相同,则k和y的值分别为(
A.1,11
B.-1,9
C.5,15
D.3,3
A
)A.1,11
B.-1,9
C.5,15
D.3,3
答案:
A
3. 根据表中一次函数的自变量x与函数值y的对应值,可得p的值为(
| x | ... | -2 | 0 | 1 | ... |
| y | ... | 3 | p | 0 | ... |

A.1
B.-1
C.3
D.-3
A
)| x | ... | -2 | 0 | 1 | ... |
| y | ... | 3 | p | 0 | ... |

A.1
B.-1
C.3
D.-3
答案:
A
4. 铁的密度为$7.9g/cm^3,$铁块的质量m(g)与它的体积$V(cm^3)$之间的函数表达式为m= 7.9V.当$V= 10cm^3$时,m=
79
g.
答案:
79
5. 如图,已知B中的实数与A中的实数之间的对应关系是某个一次函数.若用y表示B中的实数,用x表示A中的实数,则a=
1
.
答案:
1 提示:设这个一次函数的表达式为 y=kx+b(k≠0).把{x=-3,y=-9和{x=-1,y=-5代入表达式,得{-9=-3k+b,-5=-k+b,解得{k=2,b=-3.所以 y=2x-3.所以当x=(-√2)²=2时,y=2×2-3=1,即a=1.
6. 已知y是x的一次函数,且当x= -2时,y= 7;当x= 3时,y= -8.
(1) 求该一次函数的表达式.
(2) 当y≤2时,求自变量x的取值范围.
(1) 求该一次函数的表达式.
(2) 当y≤2时,求自变量x的取值范围.
答案:
解:
(1)设y=kx+b,则{-2k+b=7,3k+b=-8,解得{k=-3,b=1.所以该一次函数的表达式为y=-3x+1.
(2)因为y≤2,所以-3x+1≤2,解得x≥-1/3.所以当y≤2时,自变量x的取值范围是x≥-1/3.
(1)设y=kx+b,则{-2k+b=7,3k+b=-8,解得{k=-3,b=1.所以该一次函数的表达式为y=-3x+1.
(2)因为y≤2,所以-3x+1≤2,解得x≥-1/3.所以当y≤2时,自变量x的取值范围是x≥-1/3.
7. (2024苏州市工业园区一模)一个高为30cm的圆柱形玻璃杯中存有一定量的水,将大小相同的棋子轻轻投入该玻璃杯中,玻璃杯中水面的高度y(cm)会随着投入的棋子数x(枚)的变化而变化.根据表格中的信息,解答下列问题.
| x/枚 | 3 | 12 |
| y/cm | 12 | 15 |
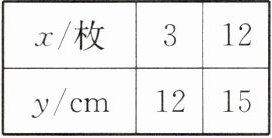
(1) 求y与x的函数表达式.
(2) 要使水不溢出玻璃杯,最多可以投入多少枚棋子?
| x/枚 | 3 | 12 |
| y/cm | 12 | 15 |

(1) 求y与x的函数表达式.
(2) 要使水不溢出玻璃杯,最多可以投入多少枚棋子?
答案:
解:
(1)由题意可知,每投入一枚棋子,水面高度上升的数量一定,所以y是x的一次函数.设一次函数表达式为y=kx+b(k,b为常数,且k≠0).将x=3,y=12和x=12,y=15代入,得{3k+b=12,12k+b=15,解得{k=1/3,b=11,所以y与x的函数表达式为y=1/3x+11.
(2)要使水不溢出玻璃杯,则1/3x+11≤30,解得x≤57.所以要使水不溢出玻璃杯,最多可以投入57枚棋子.
(1)由题意可知,每投入一枚棋子,水面高度上升的数量一定,所以y是x的一次函数.设一次函数表达式为y=kx+b(k,b为常数,且k≠0).将x=3,y=12和x=12,y=15代入,得{3k+b=12,12k+b=15,解得{k=1/3,b=11,所以y与x的函数表达式为y=1/3x+11.
(2)要使水不溢出玻璃杯,则1/3x+11≤30,解得x≤57.所以要使水不溢出玻璃杯,最多可以投入57枚棋子.
查看更多完整答案,请扫码查看


