《2025年小题狂做八年级数学上册苏科版提优版》

1. 如图 1,已知 AB⊥BD,ED⊥BD,AB= CD,BC= DE,可证得 AC⊥CE. 若将 CD 沿 CB 方向平移到图 2,3,4,5 的情形,其余条件不变,则这四种情况下,结论$“AC_1⊥C_2E”$仍然成立的有(D)
A.1 个
B.2 个
C.3 个
D.4 个

答案： D

2. 如图,在△ABC 中,AC= BC,过点 B 作射线 BF,在射线 BF 上取一点 E,连接 AE,使得∠CBF= ∠CAE,过点 C 作射线 BF 的垂线,垂足为 D. 若 DE= 1,AE= 4,则 BD 的长为(B)

A.6
B.5
C.4
D.3

答案： B 提示:连接 CE,过点 C 作 CM⊥AE,交 AE 的延长线于点 M. 因为 CD⊥BF,CM⊥AM,所以∠CDB=∠CMA=90°. 易证△CDB≌△CMA,所以 CD=CM,BD=AM. 易证 Rt△CED≌Rt△CEM,所以 DE=ME=1. 所以 BD=AM=AE+ME=AE+DE=5.

3. 如图,在△ABC 中,AB= AC,AD⊥BC 于点 D,DE⊥AB 于点 E,BF⊥AC 于点 F. 若 DE= 3 cm,则 BF= 6cm.

答案： 6 提示:根据题意,易证 Rt△ADB≌Rt△ADC(HL),所以 S△ABC=2S△ABD=AB·DE=3AB. 因为 S△ABC=1/2AC·BF,所以 1/2AC·BF=3AB. 因为 AC=AB,所以 1/2BF=3 cm,所以 BF=6 cm.

4. 如图,在四边形 ABCD 中,∠B= ∠C= 90°,AB＞CD,AD= AB+CD.
(1)利用直尺和圆规作∠ADC 的平分线 DE,交 BC 于点 E,在 AD 上截取 AF= AB,连接 AE,EF.(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,求证：
①EF= EC；
②AE⊥DE.

答案：
（1）解:作图如图所示.

（2）证明:①因为 AD=AB+DC,AD=AF+DF,AF=AB,所以 DF=DC. 因为 DE 平分∠ADC,所以∠FDE=∠CDE. 在△FED 和△CED 中,{DF=DC,∠FDE=∠CDE,DE=DE},所以△FED≌△CED(SAS),所以 EF=EC.
②因为△FED≌△CED,所以∠DEF=∠DEC,∠DFE=∠C=90°,所以∠AFE=90°=∠B. 在 Rt△AFE 和 Rt△ABE 中,{AF=AB,AE=AE},所以 Rt△AFE≌Rt△ABE(HL). 所以∠AEF=∠AEB. 所以∠AED=∠AEF+∠DEF=1/2∠BEF+1/2∠CEF=90°,所以 AE⊥DE.

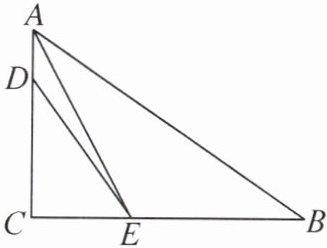
5. 如图,在 Rt△ABC 中,∠C= 90°,AE 平分∠BAC 交边 BC 于点 E,D 为边 AC 上一点,BE= DE.
(1)求证：∠B+∠EDA= 180°.
(2)求$\frac{AD+AB}{AC}$的值.

答案： （1）证明:过点 E 作 EF⊥AB 于点 F. 所以∠EFA=90°=∠C. 因为 AE 平分∠BAC,所以∠CAE=∠FAE. 易证△EAC≌△EAF(AAS),所以 EC=EF. 又因为 BE=DE,所以 Rt△ECD≌Rt△EFB(HL),所以∠EDC=∠B. 因为∠EDC+∠EDA=180°,所以∠B+∠EDA=180°.
（2）解:因为 Rt△ECD≌Rt△EFB,△EAC≌△EAF,所以 CD=FB,CA=FA,所以(AD + AB)/AC=(AC - CD+AF + FB)/AC=2AC/AC=2.