《2025年小题狂做八年级数学上册苏科版提优版》

1. 无论m为何值,直线$y= x+3m与y= -2x+6$的交点都不可能在(C)
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： C

2. 若直线$y= -2x-4与直线y= 4x+b$的交点在第三象限,则b的取值范围是-4 ＜ b ＜ 8.

答案： -4 ＜ b ＜ 8 提示:解方程组{y = -2x - 4, y = 4x + b}，得{x = -(b + 4)/6, y = (b - 8)/3}，所以{-(b + 4)/6 ＜ 0, (b - 8)/3 ＜ 0}，解得-4 ＜ b ＜ 8。

3. 如果以关于x,y的二元一次方程$x+2y-b= 0的解为坐标的点(x,y)都在直线y= -\frac {1}{2}x+b-1$上,那么常数b的值为2.

答案： 2

4. 如果方程组$\left\{\begin{array}{l} y= -x+1,\\ y= (2k+1)x-3\end{array} \right. $无解,那么直线$y= (-k+1)x-3$不经过第二象限.

答案： 二

5. 在平面直角坐标系中,无论k取何实数,直线$y= (k-1)x+4-5k$总经过定点P,则点P与动点$Q(5m-1,5m+1)$之间距离的最小值为______4√2.

答案： 4√2 提示:因为y = (k - 1)x + 4 - 5k = k(x - 5) - x + 4，所以当x = 5时，y = -1，即点P(5,-1)。因为动点Q(5m - 1,5m + 1)满足y - x = 2，即动点Q(5m - 1,5m + 1)在直线y = x + 2上。如图，过点P作直线y = x + 2的垂线，当Q为垂足时，PQ的长最短。因为点A(0,2)，B(-2,0)，所以OA = OB = 2，所以△ABO为等腰直角三角形。过点A作直线y = x + 2的垂线交x轴于点C，则△ABC为等腰直角三角形。因为AO⊥BC，所以OC = 2。设直线AC的函数表达式为y = mx + n(m ≠ 0)，代入点A(0,2)，C(2,0)，可求得m = -1，n = 2，即直线AC的函数表达式为y = -x + 2。因为AC//PQ，所以可设直线PQ的函数表达式为y = -x + b，代入点P(5,-1)，解得b = 4。联立方程组{y = x + 2, y = -x + 4}，解得{x = 1, y = 3}，所以点Q(1,3)。所以距离的最小值为PQ = √[(5 - 1)² + (-1 - 3)²] = 4√2。

6. 如图,一束光线从点O射出,照在经过点$A(1,0),B(0,1)$的镜面上的点D,经AB反射后,反射光线又照到竖立在y轴位置的镜面,经y轴再反射的光线恰好通过点A,则点D的坐标为______.

答案：
(1/3,2/3) 提示:如图，作点O关于AB的对称点O'，点A关于y轴的对称点A'。由反射的性质，可知点D在直线O'A'上，且点O'(1,1)，A'(-1,0)。易求得直线O'A'的函数表达式为y = 1/2x + 1/2。同理可得，直线AB的函数表达式为y = -x + 1。联立{y = 1/2x + 1/2, y = -x + 1}，解得{x = 1/3, y = 2/3}，所以点D的坐标为(1/3,2/3)。

7. 甲、乙两地之间有一条笔直的公路l.张老师从甲地出发沿公路l步行前往乙地,同时小亮从乙地出发沿公路l骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上张老师后两人一起步行到乙地.设张老师与乙地的距离为$y_{1}(m)$,小亮与乙地 的距离为$y_{2}(m)$,张老师与小亮之间 的距离为$s(m)$,张老师行走的时间为$x(min)$,$y_{1},y_{2}$与x之间 的函数图象如图1所示,s与x之间 的函数图象(部分)如图2所示.
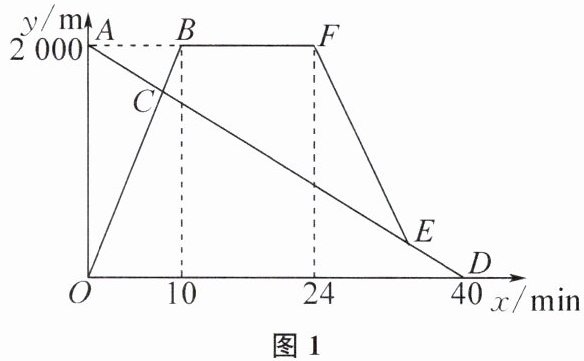
(1)求小亮从乙地到甲地的过程中,$y_{2}(m)与x(min)$之间的函数表达式.
(2)直接写出点E的坐标和它 的实际意义.(3)在图2中,补全整个过程中$s(m)与x(min)$之间 的函数图象(标注关键点 的坐标,所画图象加粗).

答案：
(1)根据题意可知，小亮从乙地到甲地对应的函数图象为线段OB，所以y2 = 200x(0 ≤ x ≤ 10)。
(2)点E的坐标为(32,400)，它的实际意义为张老师出发32 min后，被从甲地原路原速返回的小亮追上，此时他们距乙地400 m。 提示:由
(1)可知，小亮骑自行车的速度为200 m/min，所以可设直线EF的函数表达式为y = -200x + m。因为点F的坐标为(24,2000)，所以m = 6800，所以直线EF的函数表达式为y = -200x + 6800。易知线段AD的函数表达式为y = -50x + 2000(0 ≤ x ≤ 40)。联立，得{y = -50x + 2000, y = -200x + 6800}，解得{x = 32, y = 400}，所以点E的坐标为(32,400)。
(3)如图所示。