《2025年小题狂做八年级数学上册苏科版提优版》

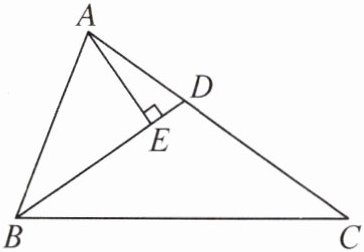
9. 如图,在△ABC 中,∠ABC= 2∠C,BD 平分∠ABC,交 AC 于点 D,AE⊥BD,垂足为 E. 求证:AC= 2BE.

答案： 证明:过点 A 作 AF//BC,交 BD 的延长线于点 F,所以∠F=∠DBC,∠FAD=∠C.因为∠ABC=2∠C,BD 平分∠ABC,所以∠ABD=∠DBC=∠C.所以∠F=∠FAD=∠ABD,BD=CD,所以 AD=DF,AB=AF.因为 AE⊥BD,所以 BE=EF=$\frac{1}{2}$BF.因为 AC=AD+CD=DF+BD=BF,所以 AC=2BE.

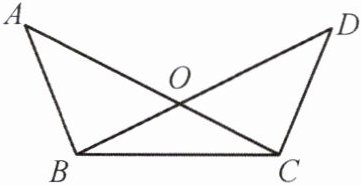
1. 如图,AC 与 BD 相交于点 O,∠A= ∠D,如果请你再补充一个条件,使得△BOC 是等腰三角形,那么你补充的条件不能是 (C)

A.OA= OD
B.AB= CD
C.∠ABO= ∠DCO
D.∠ABC= ∠DCB

答案： C

2. 如图,在△ABC 中,ED//BC,∠ABC 和∠ACB 的平分线分别交 ED 于点 G,F. 若 FG= 5,ED= 8,则 EB+DC 的值为 13.

答案： 13 提示:因为 ED//BC,所以∠EGB=∠GBC,∠DFC=∠FCB.因为 BG 平分∠ABC,CF 平分∠ACB,所以∠ABG=∠GBC,∠ACF=∠FCB,所以∠ABG=∠EGB,∠DFC=∠ACF,所以 EB=EG,DC=DF.因为 FG=5,ED=8,所以 EB+DC=EG+DF=ED+FG=5+8=13.

3. 如图,在△ABC 中,AB= AC,AB 的垂直平分线 MN 分别交 AC,AB 于点 D,E,连接 BD,DF⊥BC 于点 F. 若∠A= 36°,给出下列结论:①∠C= 72°;②△ABD 和△BCD 都是等腰三角形;③DE= DF. 其中所有正确结论的序号有 ①②③.

答案： ①②③ 提示:因为∠A=36°,AB=AC,所以∠ABC=∠C=72°,故①正确;因为 MN 是 AB 的垂直平分线,所以 AD=BD,所以△ABD 是等腰三角形,所以∠ABD=∠A=36°,所以∠CBD=∠ABC-∠ABD=36°,所以∠CDB=180°-∠CBD-∠C=72°,所以∠CDB=∠C=72°,所以 BD=BC,所以△BCD 是等腰三角形,故②正确;因为∠ABD=∠CBD=36°,DF⊥BC 于点 F,MN 是 AB 的垂直平分线,所以 DE=DF,故③正确.

4. 如图,在△ABC 中,AB= 5,AC= 3,BC= 7,AI 平分∠BAC,CI 平分∠ACB,将∠BAC 向下平移,使其顶点与点 I 重合,则图中阴影部分的周长为7.

答案： 7 提示:连接 BI,则 BI 平分∠ABC,即∠ABI=∠CBI.设∠BAC 平移后与边 BC 的交点分别为 D,E.由平移可得 AB//DI,则∠ABI=∠BID.所以∠CBI=∠BID,所以 BD=DI.同理可得 CE=EI.所以△DIE 的周长为 DE+DI+EI=DE+BD+CE=BC=7.

5. 如图,在△ABC 中,AD 平分∠BAC,BD⊥AD,垂足为 D,过点 D 作 DE//AC 交 AB 于点 E. 若 AB= 5,则线段 DE 的长为2.5.

答案： 2.5 提示:因为 AD 平分∠BAC,所以∠BAD=∠CAD.因为 DE//AC,所以∠CAD=∠ADE.所以∠BAD=∠ADE,所以 AE=DE.因为 BD⊥AD,所以∠ADB=90°,所以∠ADE+∠BDE=90°,∠BAD+∠ABD=90°.所以∠BDE=∠ABD,所以 BE=DE.所以 BE=DE=AE.因为 AB=5,所以 DE=$\frac{1}{2}$AB=2.5.

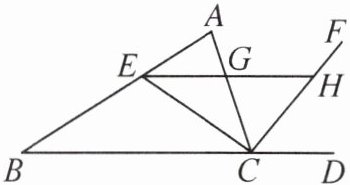
6. 如图,在△ABC 中,CE 平分∠ACB,交 AB 于点 E,EG//BC,交 AC 于点 G.
(1)求证:EG= CG.
(2)延长 EG 交 CF 于点 H,若 G 是 EH 的中点,求证:CF 平分∠ACD.

答案：
(1)证明:因为 CE 平分∠ACB,所以∠BCE=∠ACE.因为 EG//BC,所以∠BCE=∠GEC.所以∠ACE=∠GEC,所以 EG=CG.
(2)因为 G 是 EH 的中点,所以 EG=GH.因为 EG=CG,所以 CG=GH,所以∠GCH=∠GHC.由题意可知 EH//BC,所以∠GHC=∠HCD,所以∠GCH=∠HCD,所以 CF 平分∠ACD.