《2025年小题狂做八年级数学上册苏科版提优版》

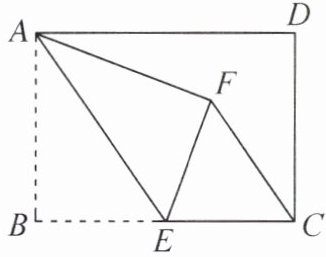
1. 如图,在长方形纸片 ABCD 中,E 为 BC 的中点,连接 AE,将$△ABE$沿 AE 所在的直线折叠得到$△AFE$,连接 CF. 若$AB= 4,BC= 6$,则 CF 的长为(D)

A.3
B.3.4
C.3.5
D.3.6

答案： D 提示:连接BF,交AE于点G.由折叠的性质,得BE=EF,AE垂直平分BF,即AE⊥BF,BG=FG.因为AB=4,BC=6,E为BC的中点,所以BE=CE=1/2BC=3.由勾股定理,得AE=√(AB²+BE²)=5.因为S△ABE=1/2AB·BE=1/2AE·BG,即1/2×4×3=1/2×5BG,解得BG=2.4,所以BF=2BG=4.8.因为CE=BE=FE,所以∠EBF=∠EFB,∠EFC=∠ECF,所以∠BFC=∠EFB+∠EFC=1/2(∠FBE+∠BFC+∠FCB)=90°.在Rt△BFC中,CF=√(BC² - BF²)=3.6.

2. (2025 南京市玄武区期末)如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形 MNPQ 拼成的一个大正方形 ABCD. 连接 AQ,BP,CN,DM. 若正方形 ABCD 的面积为 2a,阴影部分的面积为 2b,则 AN 的长为(C)
A.$a+b$
B.$a^{2}+b^{2}$
C.$\sqrt {a+b}$
D.$\sqrt {a^{2}+b^{2}}$

答案： C 提示:设MN=x,DN=AM=y,则AN=AM+MN=y+x.因为S正方形ABCD=AD²=AN²+DN²=(y+x)²+y²,所以2a=(y+x)²+y²①.因为S阴影=4S△MND+S正方形MNPQ,所以2b=4×1/2xy+x²②.1/2(①+②),得a+b=(x+y)².所以AN=√(a+b).

3. 如图,在数轴上,点 A,B 表示的数分别为 0,2,$BC⊥AB$于点 B,且$BC= 1$,连接 AC,在 AC 上截取$CD= BC$,以点 A 为圆心,AD 的长为半径画弧,交线段 AB 于点 E,则点 E 表示的实数是1.24(精确到 0.01,参考数据:$\sqrt {5}\approx 2.236$).

答案： 1.24

4. 如图,已知$△ABC与△ADC$均是直角三角形,$∠B= ∠D= 90^{\circ },BC= 6,CD= 5$. 若$∠BAC+2∠CAD= 180^{\circ }$,则 AB 的长是______7/4.

答案： 7/4 提示:延长CD,BA交于点E.因为∠BAC+∠CAD+∠DAE=180°,∠BAC+2∠CAD=180°,所以∠CAD=∠DAE.易证△CDA≌△EDA,所以AC=AE,CD=ED=5,所以CE=10.在Rt△BCE中,由勾股定理,得BE=8.设AB=x,则AC=AE=8 - x.因为AB²+BC²=AC²,所以x²+6²=(8 - x)²,解得x=7/4.所以AB的长是7/4.

5. 在$△ABC$中,$AB= 5,AC= 4,BC= 3$. 若点 P 在$△ABC$内部(含边界)且满足$PC≤PA≤PB$,则所有点 P 组成区域的面积为______.

答案：
27/32 提示:由AB=5,AC=4,BC=3,得AB²=AC²+BC²,所以△ABC为直角三角形.如图,作AB的垂直平分线EF,分别交边AB,AC于点E,F,作AC的垂直平分线DE,分别交边AC,AB于点D,E,连接BF,所以AD=CD=2,AE=5/2,∠ADE=90°.在Rt△ADE中,由勾股定理,得DE=3/2.因为点P在△ABC内部(含边界)且满足PC≤PA≤PB.当PC=PA时,点P在线段DE上;当PC＜PA时,点P在线段DE下方区域.同理当PA=PB时,点P在线段EF上;当PA＜PB时,点P在线段EF上方区域.综上所述,点P在△DEF内部(含边界).设CF=x,则BF=AF=4 - x.在Rt△BCF中,BF²=CF²+BC²,即(4 - x)²=x²+3²,解得x=7/8.所以CF=7/8,所以DF=CD - CF=9/8.所以△DEF的面积为1/2×3/2×9/8=27/32.

6. 细心观察下图,认真分析各式,然后解答下列问题:
$OA_{2}^{2}= 1^{2}+1^{2}= 2,S_{1}= \frac {1}{2};OA_{3}^{2}= (\sqrt {2})^{2}+1= 3,S_{2}= \frac {\sqrt {2}}{2};OA_{4}^{2}= (\sqrt {3})^{2}+1= 4,S_{3}= \frac {\sqrt {3}}{2};... .$
(1)请用含有 n(n 是正整数)的式子表示$OA_{n},S_{n}.$
$OA_{n}=\sqrt{n}$，$S_{n}=\frac{\sqrt{n}}{2}$
(2)$OA_{10}$的长为______.
$\sqrt{10}$
(3)求$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+... +S_{10}^{2}$的值.
$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+…+S_{10}^{2}=(\frac{1}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}+…+(\frac{\sqrt{10}}{2})^{2}=\frac{1}{4}+\frac{2}{4}+\frac{3}{4}+…+\frac{10}{4}=\frac{55}{4}$

答案：
(1)OAn=√n,Sn=√n/2.
(2)√10
(3)S₁²+S₂²+S₃²+…+S₁₀²=(1/2)²+(√2/2)²+(√3/2)²+…+(√10/2)²=1/4+2/4+3/4+…+10/4=55/4.