第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图,一架梯子AB斜靠在竖直墙上,M为梯子AB的中点,当梯子底端向左水平滑动到CD位置时,滑动过程中OM的变化规律是(
A.变小
B.不变
C.变大
D.先变小再变大
B
)A.变小
B.不变
C.变大
D.先变小再变大
答案:
B
2. (2024 盐城市亭湖区期中)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图,已知∠ACB= 90°,D为边AB的中点,点A,B对应的刻度为1,7,则CD的长为(
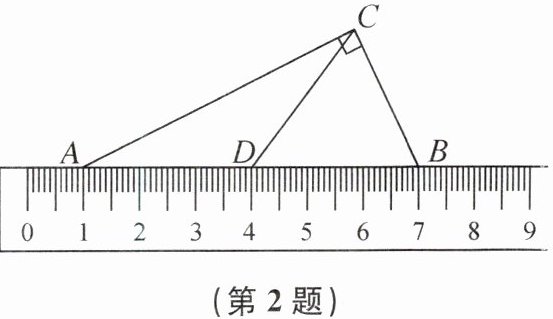
A.3.5 cm
B.3 cm
C.4.5 cm
D.6 cm
B
)
A.3.5 cm
B.3 cm
C.4.5 cm
D.6 cm
答案:
B
3. 如图,在Rt△ABC中,∠C= 90°,∠B= 30°,过点C画一条直线,将Rt△ABC分割成两个三角形,且其中至少有一个是等腰三角形,则这样的直线能画( )
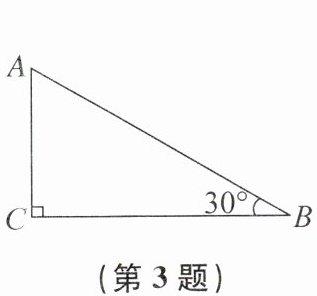
A.1条
B.2条
C.3条
D.4条

A.1条
B.2条
C.3条
D.4条
答案:
B 提示:如图,即为符合题意的等腰三角形.故这样的直线能画2条.

B 提示:如图,即为符合题意的等腰三角形.故这样的直线能画2条.

4. 如图,在Rt△ABC中,∠BAC= 90°,∠B= 36°,AD是斜边BC上的中线.将△ACD沿AD翻折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于(
A.120°
B.108°
C.72°
D.36°
B
)A.120°
B.108°
C.72°
D.36°
答案:
B 提示:因为AD是斜边BC上的中线,所以AD=BD=CD,所以∠BAD=∠B=36°,所以∠ADC=∠B+∠BAD=72°.根据折叠的性质,得∠ADF=∠ADC=72°.所以∠BED=∠BAD+∠ADF=36°+72°=108°.
5. 如图,∠AOB= 30°,OP平分∠AOB,PC//OB,PD⊥OB于点D.若PD= 2 cm,则PC=
4
cm.
答案:
4 提示:过点P作PE⊥OA于点E,则∠PEC=90°.因为OP平分∠AOB,PD⊥OB,所以PE=PD=2cm.因为PC//OB,∠AOB=30°,所以∠PCE=∠AOB=30°,所以PC=2PE=4cm.
6. 如图,已知线段AB,用两种不同的方法作一个含30°角的直角三角形ABC,使其斜边为AB.(用直尺和圆规作图,不写作法,保留作图痕迹)


答案:
解:如图1,图2,△ABC即为所求. 提示:如图1,先作线段AB的垂直平分线,交AB于点D,再分别以点A,D为圆心,AD长为半径画弧,两弧相交于点C,连接AC,BC.则△ABC即为所作.如图2,作射线AM,在射线AM上截取AC=$\frac{1}{2}$AB,过点C作AC的垂线CN,以点A为圆心,AB长为半径画弧,交CN于点B,连接AB,BC.则△ABC即为所作.


解:如图1,图2,△ABC即为所求. 提示:如图1,先作线段AB的垂直平分线,交AB于点D,再分别以点A,D为圆心,AD长为半径画弧,两弧相交于点C,连接AC,BC.则△ABC即为所作.如图2,作射线AM,在射线AM上截取AC=$\frac{1}{2}$AB,过点C作AC的垂线CN,以点A为圆心,AB长为半径画弧,交CN于点B,连接AB,BC.则△ABC即为所作.


7. 如图,在△ABC中,AD是高,CE是中线,G是CE的中点,DG⊥CE,垂足为G.
(1)试说明:DC= BE.
(2)若∠AEC= 63°,求∠BCE的度数.

(1)试说明:DC= BE.
(2)若∠AEC= 63°,求∠BCE的度数.

答案:
解:
(1)因为AD是高,所以AD⊥BC,所以∠ADB=90°.因为CE是中线,所以AE=BE.所以DE=BE=AE.因为DG⊥CE,G是CE的中点,所以DE=DC.所以DC=BE.
(2)设∠BCE=x.因为BE=DE=DC,所以∠DEC=∠DCE=x,所以∠EBD=∠BDE=∠DEC+∠DCE=2x.因为∠AEC=∠EBD+∠DCE,所以63°=3x,解得x=21°.所以∠BCE的度数为21°.
(1)因为AD是高,所以AD⊥BC,所以∠ADB=90°.因为CE是中线,所以AE=BE.所以DE=BE=AE.因为DG⊥CE,G是CE的中点,所以DE=DC.所以DC=BE.
(2)设∠BCE=x.因为BE=DE=DC,所以∠DEC=∠DCE=x,所以∠EBD=∠BDE=∠DEC+∠DCE=2x.因为∠AEC=∠EBD+∠DCE,所以63°=3x,解得x=21°.所以∠BCE的度数为21°.
查看更多完整答案,请扫码查看


