第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图,通过尺规作图,得到△COD≌△C'O'D',再利用全等三角形的性质,得到了∠AOB= ∠A'O'B',那么根据尺规作图得到△COD≌△C'O'D'的理由是(

A.SAS
B.AAS
C.SSS
D.ASA
C
)
A.SAS
B.AAS
C.SSS
D.ASA
答案:
C
2. 如图,AB= AC,BD= CD,则可推出(
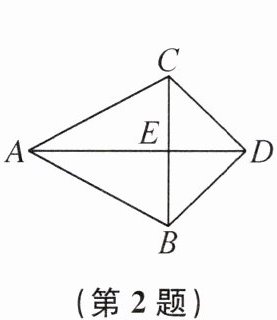
A.△BAD≌△BCD
B.△ABD≌△ACD
C.△ACD≌△BCD
D.△ACE≌△BDE
B
)
A.△BAD≌△BCD
B.△ABD≌△ACD
C.△ACD≌△BCD
D.△ACE≌△BDE
答案:
B
3. 如图,在△ABC 和△BDE 中,点 C 在边 BD 上,AC 交 BE 于点 F. 若 AC= BD,AB= ED,BC= BE,则∠ACB 等于(
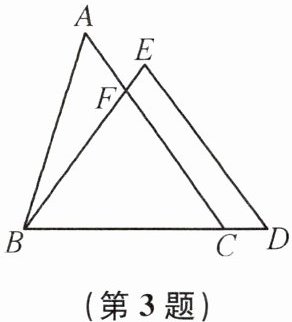
A.∠EDB
B.∠BED
C.$\frac{1}{2}∠AFB$
D.2∠ABF
C
)
A.∠EDB
B.∠BED
C.$\frac{1}{2}∠AFB$
D.2∠ABF
答案:
C 提示:易证△ABC≌△DEB,所以∠ACB=∠DBE.因为∠AFB是△BCF的外角,所以∠ACB+∠DBE=∠AFB.所以∠ACB=$\frac{1}{2}$∠AFB.
4. 有这样一道题:“如图,已知 AB= DC,DB= AC,求证:∠ABD= ∠DCA.”在证明过程中,需要添加辅助线,它的作用是
构造两个全等三角形的公共边
.
答案:
构造两个全等三角形的公共边
5. 如图,在四边形 ABCD 中,AB= CB,AD= CD,∠A= 120°,则∠B+∠D= ______.
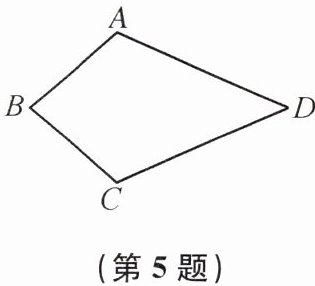

120°
答案:
120°
6. 如图,AB= AC,BD= CD. 若∠B= 28°,∠BDC= 120°,则∠A= ______.
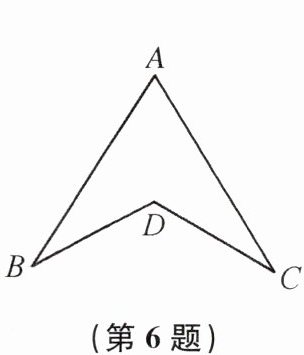

64°
答案:
64° 提示:连接AD并延长至点E.由条件,可证△ABD≌△ACD,所以∠C=∠B=28°.因为∠BDC=∠BDE+∠CDE=∠BAD+∠B+∠CAD+∠C=∠BAC+∠B+∠C,所以∠BAC=∠BDC - 2∠B=120° - 2×28°=64°.
7. 如图,在方格纸中,△ABC 的三个顶点均在格点上,这样的三角形叫作格点三角形,图中与△ABC 全等的格点三角形共有
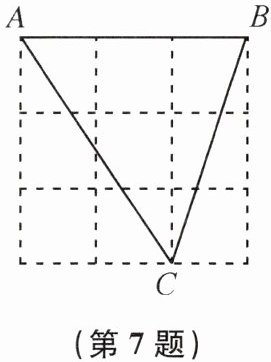
7
个.
答案:
7 提示:如图,以最大正方形的每条边为底都可作2个全等三角形,所以共有8个全等三角形.故除△ABC外有7个格点三角形与△ABC全等.
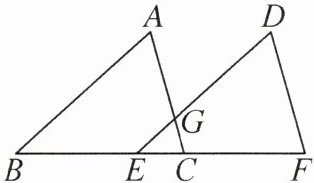
8. 如图,点 B,E,C,F 在同一直线上,AB= DE,AC= DF,BE= CF,AC 与 DE 交于点 G.
(1)求证:△ABC≌△DEF.
(2)若∠B= 40°,∠F= 70°,求∠CGE 的度数.
(1)求证:△ABC≌△DEF.
(2)若∠B= 40°,∠F= 70°,求∠CGE 的度数.

答案:
(1)证明:因为BE=CF,所以BE + EC=EC + CF,所以BC=EF.在△ABC和△DEF中,$\left\{\begin{array}{l} AB=DE,\\ AC=DF,\\ BC=EF,\end{array}\right. $所以△ABC≌△DEF(SSS).
(2)解:因为△ABC≌△DEF,所以∠GEC=∠B=40°,∠ECG=∠F=70°,所以∠CGE=180° - 40° - 70°=70°.
(1)证明:因为BE=CF,所以BE + EC=EC + CF,所以BC=EF.在△ABC和△DEF中,$\left\{\begin{array}{l} AB=DE,\\ AC=DF,\\ BC=EF,\end{array}\right. $所以△ABC≌△DEF(SSS).
(2)解:因为△ABC≌△DEF,所以∠GEC=∠B=40°,∠ECG=∠F=70°,所以∠CGE=180° - 40° - 70°=70°.
查看更多完整答案,请扫码查看


