《2025年小题狂做八年级数学上册苏科版提优版》

1. $-\sqrt{64}$ 的立方根是 (D)
A.-4
B.$\pm 4$
C.$\pm 2$
D.-2

答案： D

2. 若 $-1＜m＜0$,且 $n= \sqrt[3]{m}$,则 $m$,$n$ 的大小关系是 (A)
A.$m＞n$
B.$m＜n$
C.$m= n$
D.不能确定

答案： A

3. 一般地,如果 $x^{n}= a$($n$ 为正整数,且 $n＞1$),那么 $x$ 叫作 $a$ 的 $n$ 次方根,下列结论正确的是 (C)
A.16 的 4 次方根是 2
B.32 的 5 次方根是 $\pm 2$
C.当 $n$ 为奇数时,2 的 $n$ 次方根随 $n$ 的增大而减小
D.当 $n$ 为奇数时,2 的 $n$ 次方根随 $n$ 的增大而增大

答案： C

4. 在小于 1000 的自然数中,既不是完全平方数(平方根是整数)也不是完全立方数(立方根是整数)的数有 (C)
A.959 个
B.960 个
C.962 个
D.963 个

答案： C 提示:因为31＜$\sqrt{1000}$＜32,$\sqrt[3]{1000}$=10,所以在小于1000的自然数中,是完全平方数的有32个,是完全立方数的有10个,其中0,1,64,729都使用两次,所以所求的数有1000-(32+10-4)=962(个).

5. 已知 $x-2$ 的平方根是 $\pm 2$,$2x+y+7$ 的立方根是 3,则 $x^{2}+y^{2}$ 的平方根是±10.

答案： ±10

6. $\sqrt[3]{-\frac{1}{27}}$ 的倒数是-3,$\sqrt[3]{9}$ 的相反数是$-\sqrt[3]{9}$.

答案： -3 $-\sqrt[3]{9}$

7. 若 $\sqrt[3]{(4-k)^{3}}= k-4$,则 $k$ 的值是4.

答案： 4 提示:因为$\sqrt[3]{(4-k)^3}=k-4$,所以4-k=k-4,解得k=4.

8. 已知 $2^{a}= 27$,则 $2^{\frac{a}{3}-1}$ 的值为$\frac{3}{2}$.

答案： $\frac{3}{2}$ 提示:因为27=3³,所以2ᵃ=3³.所以$2^{\frac{a}{3}}$=$(2^a)^{\frac{1}{3}}$=$(3^3)^{\frac{1}{3}}$=3.所以$2^{\frac{a}{3}-1}$=$2^{\frac{a}{3}}$÷2=3÷2=$\frac{3}{2}$.

9. 已知 $a$,$b$互为相反数,$c$,$d$互为倒数,$e$是 $\sqrt{13}$ 的整数部分,$f$是 $\sqrt{5}$ 的小数部分,则代数式 $\sqrt{a+b}-\sqrt[3]{cd}+e-f= $4-$\sqrt{5}$.

答案： 4-$\sqrt{5}$ 提示:根据题意,得a+b=0,cd=1,e=3,f=$\sqrt{5}$-2.所以$\sqrt{a+b}-\sqrt[3]{cd}+e-f=\sqrt{0}-\sqrt[3]{1}+3-(\sqrt{5}-2)=4-\sqrt{5}$.

10. 求下列各式中 $x$ 的值:
(1)$x^{3}= 0.125$；
(2)$\frac{1}{3}(2-x)^{3}= -9$;
(3)$2(x-1)^{3}+16= 0$.

答案： 解:
(1)因为x³=0.125,所以x=0.5.
(2)因为(2-x)³=-27,所以2-x=-3,解得x=5.
(3)因为2(x-1)³=-16,所以(x-1)³=-8,所以x-1=-2,解得x=-1.

11. 如图,$a$,$b$,$c分别是数轴上点A$,$B$,$C$所对应的数,试化简:$\sqrt{b^{2}} -|a-c|+\sqrt[3]{(a+b)^{3}}$.

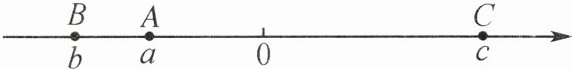
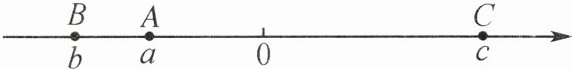
答案： 解:因为a＜0,b＜0,c＞0,所以a＜c.所以原式=|b|-|a-c|+a+b=-b+a-c+a+b=2a-c.

$12. $观察下列各式$,$并用所得出规律解决问题：　　
$(1)\sqrt{2}\approx1 .414,\sqrt{200}\approx14.14,\sqrt{20000}\approx141.4,…\sqrt{0.03}\approx0 .1732,\sqrt{3}\approx1.732,\sqrt{300}\approx17.32,…$由此可见$,$被开方数的小数点每向右移动2位$,$其算术平方根的小数点向右移动1位$.$　　
$(2)$已知$\sqrt{15}\approx3 .873,\sqrt{1 .5}\approx1.225,$则$\sqrt{150}$≈12.25;$\sqrt{0.15}$≈0.3873.
(3)$\sqrt[3]{1}= 1,\sqrt[3]{1000}= 10,\sqrt[3]{1000000}= 100$,…,小数点的变化规律被开方数的小数点向右(左)移动三位,其立方根的小数点向右(左)移动一位.
(4)$已知\sqrt[3]{10}\approx2 .154,\sqrt[3]{y}\approx-0.2154,$则y=-0.01.

答案： 解:
(1)2 右 1
(2)12.25 0.387 3
(3)被开方数的小数点向右(左)移动三位,其立方根的小数点向右(左)移动一位.
(4)-0.01