《2025年小题狂做八年级数学上册苏科版提优版》

1. 若$\triangle ABC的三边长a,b,c满足a^{2}+b^{2}+c^{2}+50= 6a+8b+10c$,则$\triangle ABC$是(B)
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形

答案： B 提示:将题中等式整理，得$(a^{2}-6a + 9)+(b^{2}-8b + 16)+(c^{2}-10c + 25)=0$，即$(a - 3)^{2}+(b - 4)^{2}+(c - 5)^{2}=0$，所以$a = 3$，$b = 4$，$c = 5$。因为$3^{2}+4^{2}=5^{2}$，所以$\triangle ABC$为直角三角形。

2. 如图是一块农家菜地的平面图,已知$AD= 4\ \text{m}$,$CD= 3\ \text{m}$,$AB= 13\ \text{m}$,$BC= 12\ \text{m}$,$\angle ADC= 90^{\circ}$,则这块菜地的面积为(A)
A.$24\ \text{m}^{2}$
B.$30\ \text{m}^{2}$
C.$36\ \text{m}^{2}$
D.$42\ \text{m}^{2}$

答案： A

3. 如果三个正整数$a,b,c满足a^{2}+b^{2}= c^{2}$,那么称$a,b,c$为一组勾股数.如果一个正整数$m能表示成两个非负整数x,y$的平方和,即$m= x^{2}+y^{2}$,那么称$m$为广义勾股数.现有下面的结论：①7 是广义勾股数；②13 是广义勾股数；③两个广义勾股数的和是广义勾股数；④两个广义勾股数的积是广义勾股数；⑤若$x= m^{2}-n^{2}$,$y= 2mn$,$z= m^{2}+n^{2}$,其中$x,y,z,m,n$是正整数,则$x,y,z$是一组勾股数.其中正确的是(D)
A.①③④⑤
B.②④
C.②③⑤
D.②④⑤

答案： D 提示:因为7不能表示成两个非负整数的平方和，故①错误；因为$13 = 2^{2}+3^{2}$，故②正确；令$m = x^{2}+y^{2}$，$n = a^{2}+b^{2}$，则$m + n = x^{2}+y^{2}+a^{2}+b^{2}$，不一定能表示成两个非负整数的平方和，故③错误；因为$mn=(a^{2}+b^{2})(x^{2}+y^{2})=a^{2}x^{2}+a^{2}y^{2}+b^{2}x^{2}+b^{2}y^{2}=(ax)^{2}+(by)^{2}+2abxy+(ay)^{2}+(bx)^{2}-2abxy=(ax + by)^{2}+(ay - bx)^{2}$，能表示成两个非负整数的平方和，故④正确；易证$x^{2}+y^{2}=z^{2}$，故⑤正确。

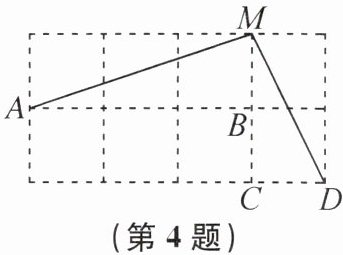
4. 如图是由边长相等的小正方形组成的网格,则$\angle MDC-\angle MAB= $45$^{\circ}$.(点$A,B,C,D,M$均在网格线交点处).

答案： 45 提示:如图，取格点E，连接ME，DE，则$\angle MAB = \angle EDF$，所以$\angle MDC - \angle MAB = \angle MDC - \angle EDF = \angle MDE$。设正方形网格中每个小正方形的边长为1，则易知$ME = MD = \sqrt{2^{2}+1^{2}}=\sqrt{5}$，$DE = \sqrt{3^{2}+1^{2}}=\sqrt{10}$，所以$ME^{2}+MD^{2}=DE^{2}$，所以$\triangle EMD$是直角三角形。又因为$ME = MD$，所以$\angle MDE = 45^{\circ}$，即$\angle MDC - \angle MAB = 45^{\circ}$。

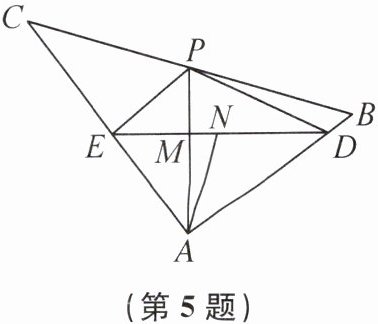
5. 如图,在$\triangle ABC中AB= 6$,$AC= 8$,$BC= 10$,$P为边BC$上一动点,连接$AP$,$DE\perp AP$,分别交$AB$,$AC于点D$,$E$,垂足为$M$,$N为DE$的中点.若四边形$ADPE$的面积为 18,则$AN$的最大值为______$\frac{15}{4}$.

答案： $\frac{15}{4}$ 提示:易得$AB^{2}+AC^{2}=BC^{2}$，所以$\triangle ABC$为直角三角形，且$\angle BAC = 90^{\circ}$。因为N为DE的中点，所以$AN = \frac{1}{2}DE$。因为四边形ADPE的面积为18，$DE\perp AP$，所以$S_{四边形ADPE}=S_{\triangle AEP}+S_{\triangle ADP}=\frac{1}{2}AP\cdot EM+\frac{1}{2}AP\cdot DM=\frac{1}{2}AP\cdot DE = AP\cdot AN$，即$AP\cdot AN = 18$。所以当AP取得最小值时，AN有最大值。因为当$AP\perp BC$时，AP的值最小，最小值为$\frac{6×8}{10}=\frac{24}{5}$，所以AN的最大值为$18÷\frac{24}{5}=\frac{15}{4}$。

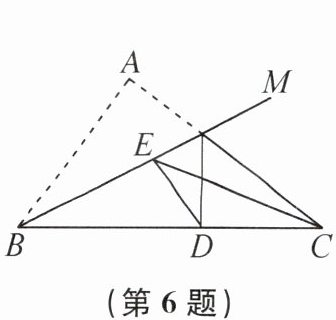
6. 如图, 在$\triangle ABC$中, $AB= 12$, $AC= 16$, $BC= 20$. 将$\triangle ABC沿射线BM$折叠, 使点$A与边BC上的点D$重合,$E为射线BM$上的一动点, 当$\triangle CDE$的周长最小时, $CE$的长为______10.

答案： 10 提示:设射线BM交AC于点F。因为$12^{2}+16^{2}=400 = 20^{2}$，即$AB^{2}+AC^{2}=BC^{2}$，所以$\triangle ABC$是直角三角形，且$\angle A = 90^{\circ}$。连接AE。由折叠的性质可知，$BD = AB = 12$，$AE = DE$，$AF = DF$，$\angle BDF = \angle BAF = 90^{\circ}$，所以$CD = BC - BD = 8$，$\angle CDF = 90^{\circ}$。因为$\triangle CDE$的周长为$CD + DE + CE = CD + AE + CE\geq CD + AC$，所以当A、E、C三点共线，即点E与点F重合时，$AE + CE$的值最小，最小值为AC的长。设$CF = x$，则$DF = AF = 16 - x$。在$Rt\triangle CDF$中，由勾股定理，得$CD^{2}=CF^{2}-DF^{2}$，即$8^{2}=x^{2}-(16 - x)^{2}$，解得$x = 10$，所以当$\triangle CDE$的周长最小时，CE的长为10。

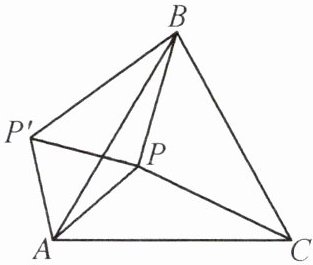
7. 如图, $P是以等边三角形ABC$内一点, 且$PA= 6$,$PB= 8$,$PC= 10$. 若将$\triangle PAC绕点A$逆时针旋转后, 得到$\triangle P'AB$.
(1) 求$PP'$的长.
(2) 求$\angle APB$的度数.
]

答案： 解:
(1)由旋转的性质，得$AP' = AP = 6$，$\angle P'AB = \angle PAC$，所以$\triangle P'AP$是等腰三角形。因为$\triangle ABC$是等边三角形，所以$\angle BAC = 60^{\circ}$，所以$\angle PAC + \angle BAP = 60^{\circ}$。所以$\angle P'AP = \angle P'AB + \angle BAP = 60^{\circ}$。所以$\triangle P'AP$是等边三角形，所以$PP' = 6$。
(2)因为$\triangle P'AP$是等边三角形，所以$\angle APP' = 60^{\circ}$。因为$PP'^{2}+PB^{2}=6^{2}+8^{2}=100 = P'B^{2}$，所以$\triangle BPP'$是直角三角形，$\angle BPP' = 90^{\circ}$。所以$\angle APB = \angle APP' + \angle BPP' = 150^{\circ}$。

8. 在$\triangle ABC$中, $BC= a$,$AC= b$,$AB= c$, 设$c$为最长边, 当$a^{2}+b^{2}= c^{2}$时,$\triangle ABC$是直角三角形; 当$a^{2}+b^{2}\neq c^{2}时利用代数式a^{2}+b^{2}和c^{2}$的大小关系,探究$\triangle ABC$的形状(按角分类).
(1) 当$\triangle ABC$的三边长分别为6,8,9时,$\triangle ABC$为锐角三角形; 当$\triangle ABC$ 的三边长分别为6,8,11时,$\triangle ABC$为钝角三角形.
(2)猜想:当$a^{2}+b^{2}$＞$c^{2}$时,$\triangle ABC$为锐角三角形,当$a^{2}+b^{2}$＜$c^{2}$时,$\triangle ABC$为钝角三角形.
(3)判断当$a= 1$,$b= 2$时,$\triangle ABC$的形状,并求出对应的$c^{2}$的取值范围.
解:根据题意及三角形的三边关系，得$2\leq c＜3$，$a^{2}+b^{2}=1^{2}+2^{2}=5$。①当$a^{2}+b^{2}＞c^{2}$，即$4\leq c^{2}＜5$时，该三角形是锐角三角形；②当$a^{2}+b^{2}=c^{2}$，即$c^{2}=5$时，该三角形是直角三角形；③当$a^{2}+b^{2}＜c^{2}$，即$5＜c^{2}＜9$时，该三角形是钝角三角形。

答案： 解:
(1)锐角 钝角
(2)$＞$ $＜$
(3)根据题意及三角形的三边关系，得$2\leq c＜3$，$a^{2}+b^{2}=1^{2}+2^{2}=5$。①当$a^{2}+b^{2}＞c^{2}$，即$4\leq c^{2}＜5$时，该三角形是锐角三角形；②当$a^{2}+b^{2}=c^{2}$，即$c^{2}=5$时，该三角形是直角三角形；③当$a^{2}+b^{2}＜c^{2}$，即$5＜c^{2}＜9$时，该三角形是钝角三角形。