第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图,A,B,C 表示三个居民小区,为了方便居民生活,现准备建一个生活超市,使它到这三个居民小区的距离相等,那么生活超市应建在 (
A.三边中线的交点
B.三条内角平分线的交点
C.三边的垂直平分线的交点
D.三边上高所在直线的交点
C
)A.三边中线的交点
B.三条内角平分线的交点
C.三边的垂直平分线的交点
D.三边上高所在直线的交点
答案:
C
2. 直角三角形三边垂直平分线的交点位于三角形的 (
A.内部
B.外部
C.斜边中点
D.不能确定
C
)A.内部
B.外部
C.斜边中点
D.不能确定
答案:
C
3. 如图,分别以 Rt△ABC 的顶点 A,B 为圆心,大于$\frac{1}{2}AB$的长为半径画弧,过两弧交点的直线交 AC 于点 D,连接 DB. 若∠A= 40°,则∠BDC 的度数为 (
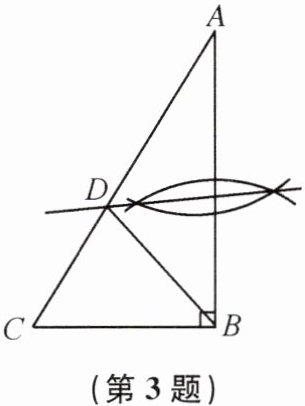
A.70°
B.75°
C.80°
D.85°
C
)
A.70°
B.75°
C.80°
D.85°
答案:
C
4. (2024 南京市玄武区期中)如图,在△ABC 中,边 AB 的垂直平分线分别交 BC,AB 于点 D,E. 若 AE= 4 cm,△ADC 的周长为 9 cm,则△ABC 的周长是
17
cm.
答案:
17
5. 如图,线段 AB 的垂直平分线与线段 BC 的垂直平分线的交点 P 恰好在 AC 上,且 AC= 10 cm,则点 B 到点 P 的距离为
5
cm.
答案:
5
6. 如图,线段 AB,BC 的垂直平分线$l_{1},l_{2}$相交于点 O,M,N 为垂足. 若∠1= 41°,则∠AOC= ______
82°
.
答案:
82° 提示:连接BO并延长至点P.因为线段AB,BC的垂直平分线l₁,l₂相交于点O,所以OA=OB,OB=OC,∠OMB=∠ONB=90°,所以∠OBA=∠A,∠OBC=∠C,∠ABC+∠MON=180°.因为∠1+∠MON=180°,所以∠ABC=∠1=41°.因为∠AOP=2∠OBA,∠COP=2∠OBC,所以∠AOC=2(∠OBA+∠OBC)=2∠ABC=82°.
7. 如图,CD 是五边形 ABCDE 的一边,若 AM 垂直平分 CD,垂足为 M,且______,______,则______.
给出下列信息:①AM 平分∠BAE;②AB= AE;③BC= DE. 请从中选择适当信息分别作为条件和结论,将对应的序号填到横线上,使之构成真命题,补全图形,并加以证明.
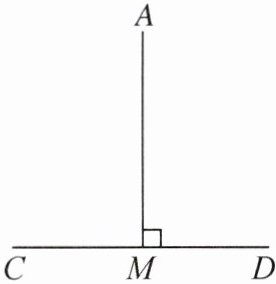
给出下列信息:①AM 平分∠BAE;②AB= AE;③BC= DE. 请从中选择适当信息分别作为条件和结论,将对应的序号填到横线上,使之构成真命题,补全图形,并加以证明.

答案:
②③ ①
证明:根据题意补全图形如图所示,连接AC,AD.因为AM垂直平分CD,所以AC=AD,∠AMC=∠AMD=90°.又因为AM=AM,所以Rt△ACM≌Rt△ADM(HL),所以∠CAM=∠DAM.在△ABC和△AED中,{AB=AE,AC=AD,BC=ED},所以△ABC≌△AED(SSS),所以∠BAC=∠EAD.所以∠BAC+∠CAM=∠EAD+∠DAM,即∠BAM=∠EAM,所以AM平分∠BAE.

(若条件选①②,结论选③,则证明如下:连接AC,AD.因为AM垂直平分CD,所以AC=AD,∠AMC=∠AMD=90°.又因为AM=AM,所以Rt△ACM≌Rt△ADM(HL),所以∠CAM=∠DAM.因为AM平分∠BAE,所以∠BAM=∠EAM,所以∠BAM - ∠CAM=∠EAM - ∠DAM,即∠BAC=∠EAD.在△ABC和△AED中,{AB=AE,∠BAC=∠EAD,AC=AD},所以△ABC≌△AED(SAS),所以BC=DE.不能由①③证得②.)
②③ ①
证明:根据题意补全图形如图所示,连接AC,AD.因为AM垂直平分CD,所以AC=AD,∠AMC=∠AMD=90°.又因为AM=AM,所以Rt△ACM≌Rt△ADM(HL),所以∠CAM=∠DAM.在△ABC和△AED中,{AB=AE,AC=AD,BC=ED},所以△ABC≌△AED(SSS),所以∠BAC=∠EAD.所以∠BAC+∠CAM=∠EAD+∠DAM,即∠BAM=∠EAM,所以AM平分∠BAE.

(若条件选①②,结论选③,则证明如下:连接AC,AD.因为AM垂直平分CD,所以AC=AD,∠AMC=∠AMD=90°.又因为AM=AM,所以Rt△ACM≌Rt△ADM(HL),所以∠CAM=∠DAM.因为AM平分∠BAE,所以∠BAM=∠EAM,所以∠BAM - ∠CAM=∠EAM - ∠DAM,即∠BAC=∠EAD.在△ABC和△AED中,{AB=AE,∠BAC=∠EAD,AC=AD},所以△ABC≌△AED(SAS),所以BC=DE.不能由①③证得②.)
查看更多完整答案,请扫码查看


