第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. (2025 南京市玄武区期末)在平面直角坐标系中,点 A 的坐标是(-2,1).将点 A 向右平移 3 个单位长度,得到点$ A_1,$再作点$ A_1$关于 x 轴的对称点,得到点$ A_2,$则点$ A_2$的坐标是 (
A.(1,1)
B.(-1,1)
C.(1,-1)
D.(-1,-1)
C
)A.(1,1)
B.(-1,1)
C.(1,-1)
D.(-1,-1)
答案:
C
2. 如果将△ABC 三个顶点的横坐标都乘以-1,纵坐标不变,则坐标变化后的三角形与原三角形的关系是 (
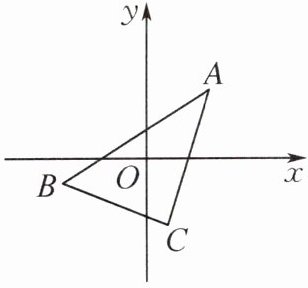
A.关于 x 轴对称
B.关于 y 轴对称
C.将原图形沿 x 轴的负方向平移了 1 个单位长度
D.将原图形沿 y 轴的负方向平移了 1 个单位长度
B
)
A.关于 x 轴对称
B.关于 y 轴对称
C.将原图形沿 x 轴的负方向平移了 1 个单位长度
D.将原图形沿 y 轴的负方向平移了 1 个单位长度
答案:
B
3. 已知点 M(1-2m,m-1)关于 x 轴的对称点在第一象限,则实数 m 的取值范围在数轴上表示正确的是 (
]
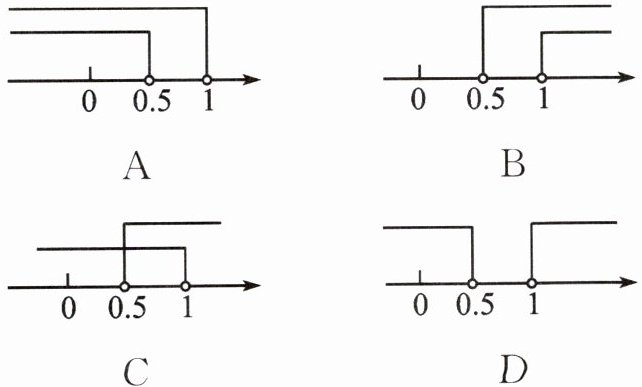
A
)]

答案:
A
4. (2025 南京市建邺区期末)在平面直角坐标系中,若点 P(2,n)与点 Q(m,-3)关于 y 轴对称,则 m+n=
-5
.
答案:
-5
5. 已知点 A 的坐标为(√2,0),把点 A 绕着坐标原点顺时针旋转 135°到点 B,那么点 B 的坐标是______.
答案:
(-1,-1) 提示:如图,过点 B 作 BC⊥y 轴于点 C. 因为点 A(√2,0),所以 OA=√2. 因为∠AOB=135°,所以∠BOC=45°,所以 OC=BC. 又因为 OB=OA=√2,OC²+BC²=OB²,所以 BC=OC=1. 因为点 B 在第三象限,所以点 B(-1,-1).
(-1,-1) 提示:如图,过点 B 作 BC⊥y 轴于点 C. 因为点 A(√2,0),所以 OA=√2. 因为∠AOB=135°,所以∠BOC=45°,所以 OC=BC. 又因为 OB=OA=√2,OC²+BC²=OB²,所以 BC=OC=1. 因为点 B 在第三象限,所以点 B(-1,-1).

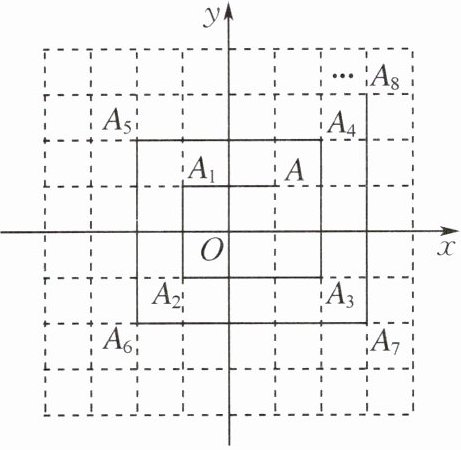
6. 如图,在平面直角坐标系中,点 A(1,1),对其进行轴对称和平移运动:点 A 关于 y 轴的对称点为$ A_1,$点$ A_1$关于 x 轴的对称点为$ A_2,$点$ A_2$向右平移 3 个单位长度得到点$ A_3,$点$ A_3$向上平移 3 个单位长度得到点$ A_4,$点$ A_4$关于 y 轴的对称点为$ A_5,$点$ A_5$关于 x 轴的对称点为$ A_6,$点$ A_6$向右平移 5 个单位长度得到点$ A_7,$点$ A_7$向上平移 5 个单位长度得到点$ A_8……$以此规律,点$ A_{99}$的坐标为______.
]
]

(26,-25)
答案:
(26,-25) 提示:由题意可知,点 A(1,1),A₄(2,2),A₈(3,3),…,所以点 A₄ₙ(n+1,n+1). 从点 A₃到点 A₄:向上平移 3 个单位长度;从 A₇到点 A₈:向上平移 5 个单位长度……依次类推,从点 A₄ₙ₋₁到点 A₄ₙ:向上平移(2n+1)个单位长度. 因为100÷4=25,所以点 A₁₀₀的坐标为(26,26),所以点 A₉₉向上平移2×25+1=51个单位长度,得到点 A₁₀₀. 所以点 A₉₉的坐标为(26,-25).
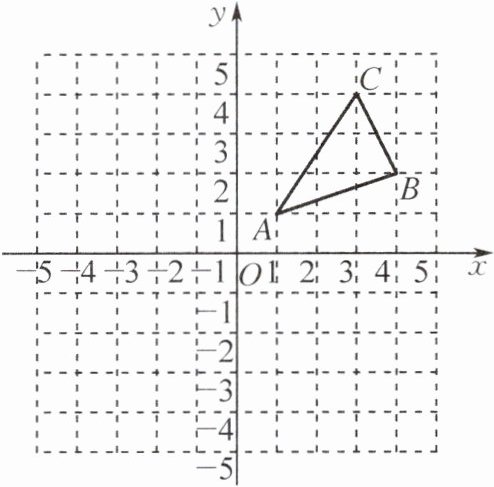
7. 如图,△ABC 三个顶点的坐标分别为 A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC 关于 x 轴对称的图形$△A_1B_1C_1.$
(2) 若△ABC 经过平移后得到$△A_2B_2C_2,$其中点$ A_2$的坐标是(-4,0),则点$ C_2$的坐标是______.
(3) 若 BE⊥x 轴于点 E,在 x 轴上存在点 P,使∠APO= ∠BPE.请在平面直角坐标系中找出点 P 的位置(保留作图痕迹),并写出点 P 的坐标:______.
]
(1) 请画出△ABC 关于 x 轴对称的图形$△A_1B_1C_1.$
(2) 若△ABC 经过平移后得到$△A_2B_2C_2,$其中点$ A_2$的坐标是(-4,0),则点$ C_2$的坐标是______.
(3) 若 BE⊥x 轴于点 E,在 x 轴上存在点 P,使∠APO= ∠BPE.请在平面直角坐标系中找出点 P 的位置(保留作图痕迹),并写出点 P 的坐标:______.
]

答案:
(1)如图,△A₁B₁C₁即为所求.
(2)(-2,3)
(3)如图,点 P 即为所求. (2,0) 提示:连接 BB₁. 因为点 B 与点 B₁关于 x 轴对称,所以 BB₁⊥x 轴,垂足为 E. 连接 AB₁交 x 轴于点 P,连接 BP. 易知∠B₁PE=∠BPE. 因为∠APO=∠B₁PE,所以∠APO=∠BPE. 此时点 P(2,0).
(1)如图,△A₁B₁C₁即为所求.
(2)(-2,3)
(3)如图,点 P 即为所求. (2,0) 提示:连接 BB₁. 因为点 B 与点 B₁关于 x 轴对称,所以 BB₁⊥x 轴,垂足为 E. 连接 AB₁交 x 轴于点 P,连接 BP. 易知∠B₁PE=∠BPE. 因为∠APO=∠B₁PE,所以∠APO=∠BPE. 此时点 P(2,0).

查看更多完整答案,请扫码查看


