第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
8. (2024 南京市秦淮区期中)如图,在△ABC 中,AB= AC,AD 平分∠BAC,FE 是 AC 的垂直平分线,交 AD 于点 F,连接 BF. 求证:AF= BF.


答案:
证明:连接CF.因为AD平分∠BAC,所以∠BAD=∠CAD.又因为AB=AC,AD=AD,所以△ADB≌△ADC.所以BD=CD,所以点D在线段BC的垂直平分线上.因为AB=AC,所以点A在线段BC的垂直平分线上.所以AD垂直平分BC,所以BF=CF.因为FE垂直平分AC,所以AF=CF,所以AF=BF.
1. (2024 无锡市江阴市期中)在正方形网格中,△ABC 的位置如图所示,且顶点均在格点上,在△ABC 内部有 E,F,G,H 四个格点,到△ABC 三个顶点距离相等的是 (
A.点 E
B.点 F
C.点 G
D.点 H
B
)A.点 E
B.点 F
C.点 G
D.点 H
答案:
B
2. 在△ABC 中,BC= 10,AB 的垂直平分线与 AC 的垂直平分线分别交 BC 于点 D,E,且 DE= 4,则 AD+AE 的值为 ( )
A.6
B.14
C.6 或 14
D.8 或 12
A.6
B.14
C.6 或 14
D.8 或 12
答案:
C 提示:连接AD,AE,则由条件可知AD=BD,AE=EC.分两种情况:如图1,当BD与CE无重合时,AD+AE=BD+CE=BC - DE=6;如图2,当BD与CE有重合时,AD+AE=BD+CE=BC+DE=14.


C 提示:连接AD,AE,则由条件可知AD=BD,AE=EC.分两种情况:如图1,当BD与CE无重合时,AD+AE=BD+CE=BC - DE=6;如图2,当BD与CE有重合时,AD+AE=BD+CE=BC+DE=14.


3. 如图,在△ABC 中,∠BAC>90°,AB 的垂直平分线交 AB 于点 D,交 BC 于点 E,AC 的垂直平分线交 AC 于点 F,交 BC 于点 G. 若以 BE,EG,GC 为边的三角形的面积为 8,则△ABC 的面积可能是 (
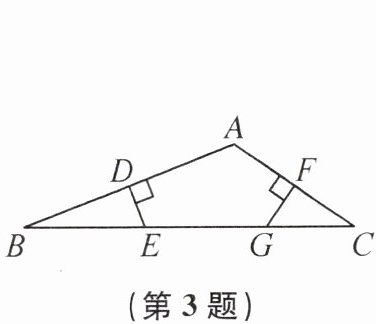
A.12
B.14
C.16
D.18
D
)
A.12
B.14
C.16
D.18
答案:
D 提示:连接AE,AG.根据线段垂直平分线的性质可得EA=EB,GA=GC.根据三角形的三边关系可得AE+AG>EG,所以BE+CG>EG.所以S△AEB+S△ACG>S△AEG,所以S△ABC>2S△AEG=16.
4. 如图,△ABC 是三边都不相等的三角形,BP 平分∠ABC,CP 平分∠ACB,BP,CP 交于点 P,O 是三边垂直平分线的交点. 当点 P,O 同时在△ABC 的内部时,∠BOC 和∠BPC 的数量关系是∠BOC=
4∠BPC - 360°
.
答案:
4∠BPC - 360° 提示:由题意,得∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,所以∠BPC=180°-(∠PBC+∠PCB)=180° - $\frac{1}{2}$(∠ABC+∠ACB)=180° - $\frac{1}{2}$(180° - ∠BAC)=90° + $\frac{1}{2}$∠BAC,即∠BAC=2∠BPC - 180°.连接AO.因为O是这个三角形三边垂直平分线的交点,所以OA=OB=OC,所以∠OAB=∠OBA,∠OAC=∠OCA,所以∠AOB=180° - 2∠OAB,∠AOC=180° - 2∠OAC,所以∠BOC=360°-(∠AOB+∠AOC)=360°-(180° - 2∠OAB+180° - 2∠OAC)=2∠OAB+2∠OAC=2∠BAC=2(2∠BPC - 180°)=4∠BPC - 360°.
5. 已知直线 l 及其两侧的两点 A,B.
(1) 在图1中的直线 l 上作一点 P,使 PA= PB,并说明理由.
(2) 在图2中的直线 l 上作一点 Q,使 l 平分∠AQB,并说明理由.

(1) 在图1中的直线 l 上作一点 P,使 PA= PB,并说明理由.
(2) 在图2中的直线 l 上作一点 Q,使 l 平分∠AQB,并说明理由.

答案:
解:
(1)如图1,连接AB,作线段AB的垂直平分线CD,交直线l于点P,P即为所求作的点.理由如下:因为直线CD是线段AB的垂直平分线,且P是CD上的点,所以PA=PB.
(2)如图2,作点B关于直线l的对称点B',连接B'A并延长,交直线l于点Q,连接BQ,Q即为所求作的点.理由如下:在直线l上任意找一点D(不与点Q重合),连接B'D,BD.因为B与B'两点关于直线l对称,所以直线l是BB'的垂直平分线,所以BD=B'D,BQ=B'Q.又因为DQ=DQ,所以△BDQ≌△B'DQ(SSS),所以∠BQD=∠B'QD,即直线l平分∠AQB.


解:
(1)如图1,连接AB,作线段AB的垂直平分线CD,交直线l于点P,P即为所求作的点.理由如下:因为直线CD是线段AB的垂直平分线,且P是CD上的点,所以PA=PB.
(2)如图2,作点B关于直线l的对称点B',连接B'A并延长,交直线l于点Q,连接BQ,Q即为所求作的点.理由如下:在直线l上任意找一点D(不与点Q重合),连接B'D,BD.因为B与B'两点关于直线l对称,所以直线l是BB'的垂直平分线,所以BD=B'D,BQ=B'Q.又因为DQ=DQ,所以△BDQ≌△B'DQ(SSS),所以∠BQD=∠B'QD,即直线l平分∠AQB.


6. 如图,AB= CD,AC,BD 的垂直平分线 EM,EN 相交于点 E. 求证:∠ABE= ∠CDE.
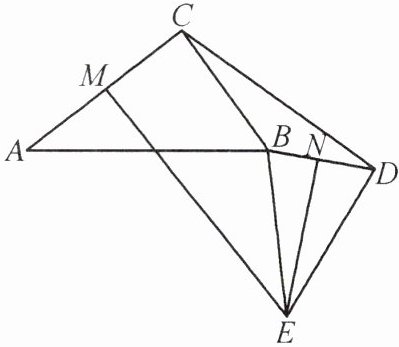

答案:
证明:连接AE,CE.因为AC,BD的垂直平分线EM,EN相交于点E,所以AE=CE,BE=DE.在△ABE和△CDE中,{AB=CD,AE=CE,BE=DE},所以△ABE≌△CDE(SSS),所以∠ABE=∠CDE.
查看更多完整答案,请扫码查看


